Network Data Analysis
- 강의자료 다운로드: click me
데이터 사이언스 현장에서는 객체 간 연결 관계를 분석하는 일이 점차 중요해지고 있다. 소셜 미디어 친구 관계, 물류 이동 경로, 추천 시스템의 유사도 그래프 등은 모두 네트워크 데이터로 표현할 수 있으며, 이 구조를 이해하면 단순 표 형태 분석보다 훨씬 깊은 인사이트를 얻을 수 있다.
이번 주차에서는 그래프 데이터의 기본 구성 요소부터 중심성 분석, 시각화 기법까지 단계적으로 정리한다. 실습에서는 networkx, pandas, pyvis 등을 활용해 작은 예제 네트워크를 직접 생성하고 분석한다.
학습 목표
-
노드(Node), 엣지(Edge), 가중치(Weight) 등 그래프 데이터의 핵심 개념을 설명할 수 있다.
-
대표적인 중심성 지표(차수, 매개, 고유벡터, 페이지랭크)의 의미와 해석 방법을 이해한다.
-
실제 네트워크 데이터를 전처리하여 구조적 특징을 탐색하고 시각화할 수 있다.
-
파이썬의
networkx라이브러리를 이용해 간단한 네트워크 분석 파이프라인을 구현한다. -
분석 목적에 따라 적절한 시각화 기법(정적/인터랙티브)을 선택하고 결과를 해석한다.
Check Point: 주어진 연결 데이터셋을 그래프로 변환하여 주요 중심성 지표를 계산하고, 전반적인 네트워크 구조를 시각적으로 설명할 수 있는가?
네트워크 데이터 이해하기
그래프 데이터 구조

-
노드(Node) 분석 대상의 개별 객체. 사람, 도시, 제품 등 상황에 따라 다양한 의미를 가진다.
-
엣지(Edge) 노드 간 관계를 나타내는 연결선. 방향성 여부(Directed/Undirected)에 따라 의미가 크게 달라지며, 가중치가 포함되면 관계의 강도나 비용을 표현할 수 있다.
-
속성(Attribute) 노드나 엣지가 가진 부가 정보. 예를 들어 사람 노드의 나이, 도시 간 이동 거리 등이 여기에 해당한다.
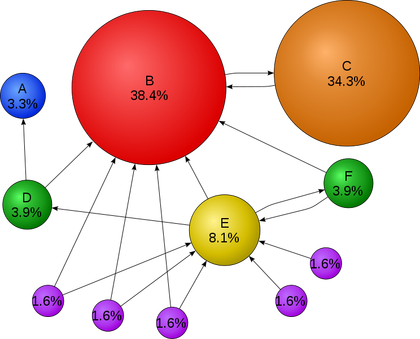
네트워크 데이터는 보통 다음 세 가지 형태로 수집된다.
| 데이터 형태 | 설명 | 예시 |
|---|---|---|
| 엣지 리스트 (Edge List) |
각 행이 두 노드의 연결을 의미 | source,target,weight |
| 인접 행렬 (Adjacency Matrix) |
행/열이 노드를 나타내고 요소가 연결 여부를 표시 | 소규모 고정 네트워크 |
| 이벤트 로그 (Interaction Log) |
시간 순서 이벤트를 관계로 해석 | 메시지 전송 기록, API 호출 로그 |
NetworkX 패키지 소개
networkx는 그래프(네트워크) 데이터를 분석하고 시각화하기 위한 파이썬 대표 라이브러리이다.
소셜 네트워크, 물류 네트워크, 통신망, 웹 링크 구조 등 객체 간의 관계 데이터를 표현하고 분석할 때 유용하다.
주요 특징
- 데이터 구조:
Graph,DiGraph,MultiGraph등 다양한 형태 지원 - 분석 기능: 중심성, 커뮤니티 탐지, 경로 탐색, 연결 성분 분석 등
- 시각화 기능:
matplotlib또는pyvis등과 연동 가능 - 유연성:
pandas,numpy,scipy등과 자연스럽게 호환
자주 사용하는 클래스
| 클래스 | 설명 | 예시 |
|---|---|---|
Graph() |
무방향 그래프 (기본형) | 친구 관계, 상호 협력 |
DiGraph() |
방향 그래프 | 이메일 발송, 링크 구조 |
MultiGraph() |
중복 엣지를 허용하는 무방향 그래프 | 두 사람 간 여러 거래 |
MultiDiGraph() |
중복 엣지 + 방향 포함 | 반복 메시지, 교차 경로 |
주요 함수 및 파라미터
| 함수 | 주요 파라미터 | 설명 |
|---|---|---|
add_node(node, **attr) |
node: 노드 이름attr: 속성(딕셔너리 형태) |
노드 추가 시 속성 지정 가능 |
add_edge(u, v, **attr) |
u, v: 연결할 노드attr: 엣지 속성 (예: weight) |
엣지 추가 및 가중치 설정 |
from_pandas_edgelist(df, source, target, edge_attr=None, create_using=nx.Graph()) |
df: 데이터프레임source/target: 컬럼 이름edge_attr: 가중치 컬럼 |
pandas 엣지리스트로부터 그래프 생성 |
from_numpy_matrix(matrix) |
matrix: 인접 행렬(numpy 배열) |
인접 행렬로부터 그래프 구성 |
from_scipy_sparse_array(matrix, create_using=nx.Graph()) |
matrix: 희소 행렬create_using: 그래프 타입 |
대용량 네트워크 처리용 |
degree(weight=None) |
weight: 가중치 컬럼 지정 |
노드의 연결 수(차수) 계산 |
neighbors(node) |
node: 기준 노드 |
인접 노드 리스트 반환 |
subgraph(nodes) |
nodes: 선택 노드 리스트 |
부분 그래프 생성 |
to_pandas_edgelist(G) |
G: 그래프 |
엣지 리스트를 pandas 데이터프레임으로 변환 |
예시 코드
import networkx as nx
import pandas as pd
# 엣지 리스트로 그래프 생성
df = pd.DataFrame({
"source": ["A", "A", "B", "C"],
"target": ["B", "C", "D", "D"],
"weight": [3, 5, 2, 1]
})
G = nx.from_pandas_edgelist(
df,
source="source",
target="target",
edge_attr="weight",
create_using=nx.DiGraph()
)
# 기본 정보 출력
print("노드 수:", G.number_of_nodes())
print("엣지 수:", G.number_of_edges())
print("노드 목록:", list(G.nodes()))
print("엣지 목록:", list(G.edges(data=True)))
실행 결과
노드 수: 4
엣지 수: 4
노드 목록: ['A', 'B', 'C', 'D']
엣지 목록: [('A', 'B', {'weight': 3}), ('A', 'C', {'weight': 5}),
('B', 'D', {'weight': 2}), ('C', 'D', {'weight': 1})]
네트워크 데이터 전처리
네트워크(Graph) 데이터는 노드와 엣지가 연결된 형태이기 때문에, 규모가 커질수록 메모리, 연산 비용, 분석 난이도가 매우 크게 증가한다. 따라서 전처리는 선택이 아니라 필수 단계이다.
메모리 및 계산 자원 한계
-
노드 수가 수백만, 엣지가 수천만 이상이 되면 그래프 연산은 매우 무거워진다.
-
Centrality, Community Detection, PageRank 등의 알고리즘은 연산 복잡도가 커서 전처리 없이는 실행 시간이 과도하게 길어지거나 실패할 수 있다.
전처리는 데이터 크기를 줄여 분석 가능하도록 만드는 과정이다.
노이즈 제거로 분석 품질 향상
-
실제 네트워크 데이터에는 스팸 노드, 의미 없는 연결, 오류 데이터가 포함될 수 있다.
-
이러한 노이즈는 분석 결과를 왜곡시키고 모델 성능을 떨어뜨릴 수 있다.
-
예시: 단 한 번만 연결된 고립 노드가 지나치게 많으면 군집 분석과 중심성 평가 결과가 의미를 잃을 수 있음
해석 가능한 구조로 단순화
-
현실의 네트워크는 그래프 전체를 보면 매우 복잡해 핵심 관계를 파악하기 어려울 수 있다.
-
전처리를 통해 구조를 단순화하면 패턴과 인사이트가 선명해진다.
전처리 작업 효과 하위 네트워크 추출 분석 목적에 맞는 부분에 집중 주요 노드 필터링 핵심 구조만 남기기 의미 있는 관계만 유지 인사이트 도출 용이
알고리즘 적용 가능성 확보
-
많은 그래프 알고리즘은 특정 조건에서만 제대로 동작한다.
알고리즘 문제점 전처리 필요성 Community Detection 희박한 그래프에서 성능 저하 밀도 조정 필요 PageRank 고립 노드가 많으면 점수 왜곡 불필요 노드 제거 필요 GNN(Graph Neural Network) 대규모 전체 그래프 입력 불가 샘플링 또는 축소 필요
전처리가 없다면 알고리즘이 실행되지 않거나 부정확한 결과가 나올 수 있다.
시각화 가능한 수준으로 축소
-
네트워크 시각화는 약 5,000 노드를 넘어가면 이해하기 어려워진다.
-
100,000 노드 이상의 그래프는 시각적으로 의미를 파악하기 어렵다.
필요한 전처리 예시
-
노드 또는 엣지 추출 및 집계
-
군집 기반 그래프 압축
-
대표 노드 중심 시각화 기법 적용
네트워크 데이터 전처리 실습
-
실습 데이터 추천: Email Networks (Kaggle)
-
직접 다운로드: email-Enron.mtx (Matrix Market 형식, 희소행렬 데이터 저장 형식)
-
관련 패키지 설치
pip install networkx scipy
import networkx as nx
from scipy.io import mmread
def print_graph_info(graph, info: str = "Graph"):
"""그래프의 기본 정보를 출력하는 유틸리티 함수"""
print(f"\n---- {info} ----")
print(f"Graph Type: {graph.__class__.__name__}")
print(f"Number of nodes: {graph.number_of_nodes():,}")
print(f"Number of edges: {graph.number_of_edges():,}")
# Matrix Market 형식(.mtx) 파일을 희소 행렬로 읽어온다.
# .tocsr: 불러온 그래프를 압축된 희소 행렬(Compressed Sparse Row format)로 변환하는 메서드
matrix = mmread("email-Enron.mtx").tocsr()
# 방향 그래프로 변환한다. (무방향 그래프가 필요하면 nx.Graph() 사용)
G: nx.DiGraph = nx.from_scipy_sparse_array(
matrix,
create_using=nx.DiGraph()
)
print_graph_info(G, "Original Graph")
실행 결과
---- Original Graph ----
Graph Type: DiGraph
Number of nodes: 36,692
Number of edges: 367,662
-
노드 36,692개는 Enron 이메일 네트워크에 참여한 이메일 계정을 의미한다.
-
엣지 183,831개는 특정 계정에서 다른 계정으로 발송된 이메일을 나타내며, 방향 정보가 포함되어 있음을 보여준다.
-
비교적 많은 엣지가 존재하므로, 우선 불필요한 자기 연결이나 중복 엣지를 정리한 뒤 중심성 분석 및 커뮤니티 탐지에 활용하는 것이 좋다.
-
식별자 정리: 노드 ID가 문자열/숫자로 혼재되어 있으면 일관된 형식으로 변환한다.
-
중복 및 자기 연결 제거: 의미 없는 자기 연결(Self-loop)이나 중복 엣지를 제거하거나 병합한다.
-
가중치/방향성 설정: 분석 목적에 맞춰 가중치를 합산하거나 평균 내며, 필요한 경우 무방향 그래프로 변환한다.
-
부분 그래프 추출: 거대한 네트워크에서는 관심 영역만 추출해 분석하거나 연결 성분을 기준으로 나누어 본다.
-
부분 그래프 추출 코드
'''
앞 코드에 이어서 작성
'''
# 네트워크가 너무 크면, 우선 분석하기 좋은 크기의 부분 그래프를 만든다.
# 예시 1: 최대 연결 성분만 추출 (비연결 그래프라면 가장 큰 연결 덩어리만 사용)
largest_component_nodes = max(nx.weakly_connected_components(G), key=len)
G_largest = G.subgraph(largest_component_nodes).copy()
print_graph_info(G_largest, "Largest Connected Component")
# 예시 2: 관심 있는 상위 중심성 노드만 남겨 집중 분석
degree_scores = dict(G_largest.degree())
top_k = 1000 # 유지할 노드 수를 상황에 맞게 조정
top_nodes = sorted(
degree_scores,
key=degree_scores.get,
reverse=True
)[:top_k]
G_focus = G_largest.subgraph(top_nodes).copy()
print_graph_info(G_focus, "Focused Subgraph")
실행 결과
----- Original Graph -----
Graph Type: DiGraph
Number of nodes: 36,692
Number of edges: 367,662
----- Largest Connected Component -----
Graph Type: DiGraph
Number of nodes: 33,696
Number of edges: 361,622
----- Focused Subgraph -----
Graph Type: DiGraph
Number of nodes: 1,000
Number of edges: 66,920
-
원본 그래프(노드
36,692개, 엣지183,831개)에서 최대 연결 성분만 추리면 약3,000개의 고립 노드·소규모 성분이 제거되어 더 응집된 구조만 남는다. -
최대 연결 성분은 노드
33,696개, 엣지361,622개를 유지하므로, 전체 활동량 대부분이 하나의 거대한 커뮤니케이션 덩어리에 집중되어 있음을 보여준다. 이후 중심성·커뮤니티 분석을 수행할 때 잡음이 줄어들고, 실제로 활발히 상호작용하는 사용자 집합에 집중할 수 있다. -
상위 중심성 노드
1,000개로 만든 부분 그래프는 엣지33,460개를 유지하여 규모는 줄지만, 핵심 사용자들의 상호 연결을 집중적으로 분석할 수 있게 해 준다.
부분 그래프 전후 비교 시각화
-
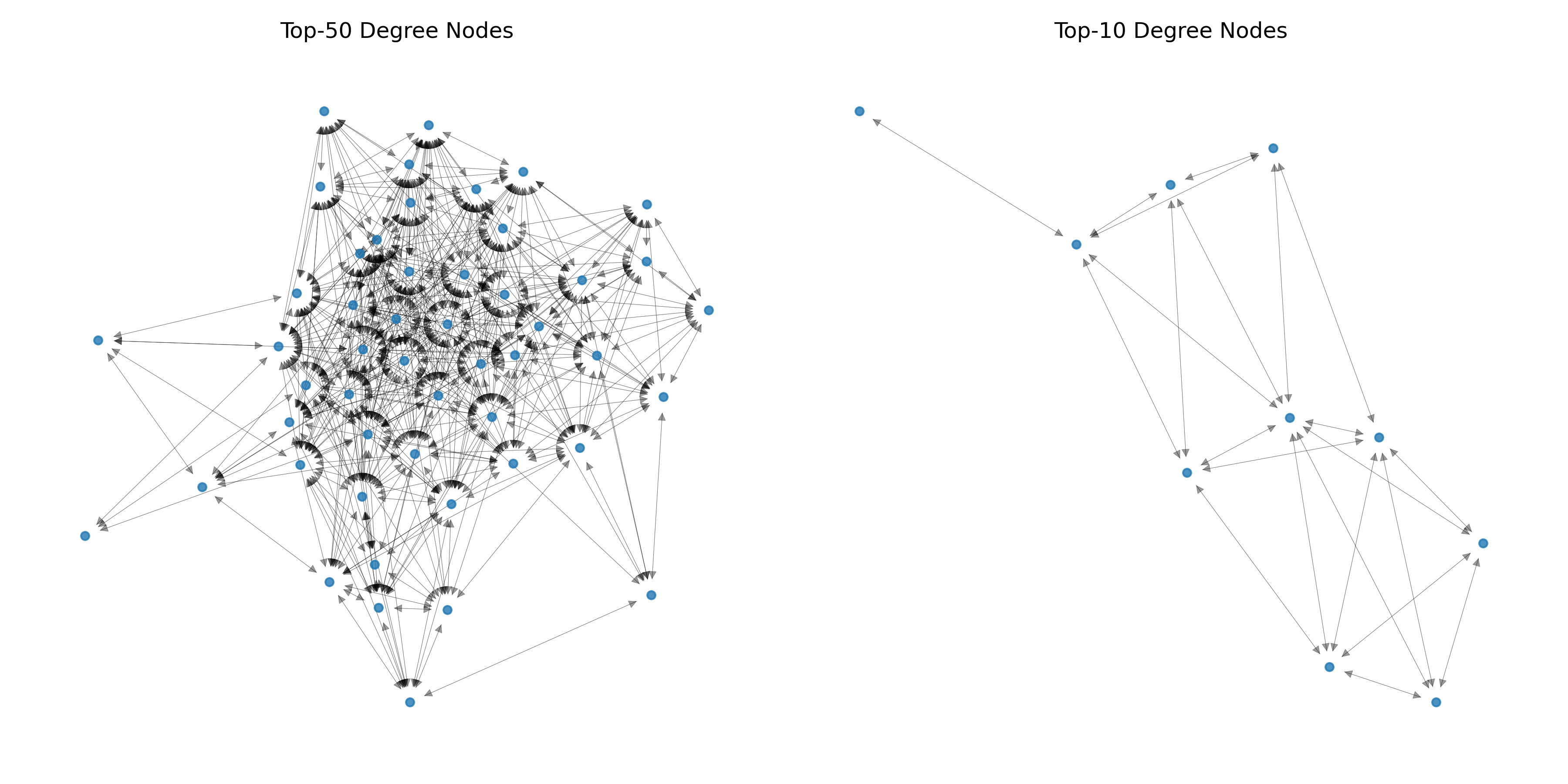
아래 코드는 전체 그래프에서 최대 연결 성분만 남긴 뒤, 차수 중심성 기준 상위 노드만을 각각 50개, 10개씩 추출하여 두 개의 서브그래프를 만든다.
-
각 서브그래프에 동일한 spring layout을 적용해 앞서 계산한 핵심 노드들의 밀집 구역을 시각적으로 비교함으로써, 노드 필터링이 구조에 어떤 변화를 주었는지 설명할 수 있다.
-
이렇게 시각화 결과와 요약 통계를 함께 제시하면 "왜 이 부분만 남겼는가"에 대한 근거를 제시할 수 있어, 보고서나 발표 자료에서 추출 전략을 설득력 있게 전달할 수 있다.
그래프 시각화 코드
import matplotlib.pyplot as plt
import networkx as nx
from scipy.io import mmread
def print_graph_info(graph, info: str = "Graph"):
"""그래프의 기본 정보를 출력하는 유틸리티 함수"""
print(f"\n---- {info} ----")
print(f"Graph Type: {graph.__class__.__name__}")
print(f"Number of nodes: {graph.number_of_nodes():,}")
print(f"Number of edges: {graph.number_of_edges():,}")
# Matrix Market 형식(.mtx) 파일을 희소 행렬로 읽어온다.
# .tocsr: 불러온 그래프를 압축된 희소 행렬(Compressed Sparse Row format)로 변환하는 메서드
matrix = mmread("email-Enron.mtx").tocsr()
# 방향 그래프로 변환한다. (무방향 그래프가 필요하면 nx.Graph() 사용)
G: nx.DiGraph = nx.from_scipy_sparse_array(
matrix,
create_using=nx.DiGraph()
)
print_graph_info(G, "Original Graph")
# 네트워크가 너무 크면, 우선 분석하기 좋은 크기의 부분 그래프를 만든다.
# 예시 1: 최대 연결 성분만 추출 (비연결 그래프라면 가장 큰 연결 덩어리만 사용)
largest_component_nodes = max(nx.weakly_connected_components(G), key=len)
G_largest = G.subgraph(largest_component_nodes).copy()
print_graph_info(G_largest, "Largest Connected Component")
# 상위 중심성 노드를 여러 크기로 추출해 비교
degree_scores = dict(G_largest.degree())
sorted_nodes = sorted(
degree_scores,
key=degree_scores.get,
reverse=True
)
subgraph_specs = [
("Top-50 Degree Nodes", 50),
("Top-10 Degree Nodes", 10),
]
subgraphs = []
for label, k in subgraph_specs:
target_nodes = sorted_nodes[:min(k, len(sorted_nodes))]
subgraph = G_largest.subgraph(target_nodes).copy()
print_graph_info(subgraph, label)
subgraphs.append((label, subgraph))
fig, axes = plt.subplots(1, len(subgraphs), figsize=(12, 6))
for ax, (label, subgraph) in zip(axes, subgraphs):
pos = nx.spring_layout(subgraph, seed=42)
nx.draw_networkx_nodes(subgraph, pos, ax=ax, node_size=20, node_color="#1f78b4", alpha=0.8)
nx.draw_networkx_edges(subgraph, pos, ax=ax, width=0.2, alpha=0.4)
ax.set_title(label)
ax.axis("off")
plt.tight_layout()
# plt.savefig("./subgraph_comparison.png", dpi=300)
# plt.close(fig)
plt.show()
중심성(Centrality) 분석
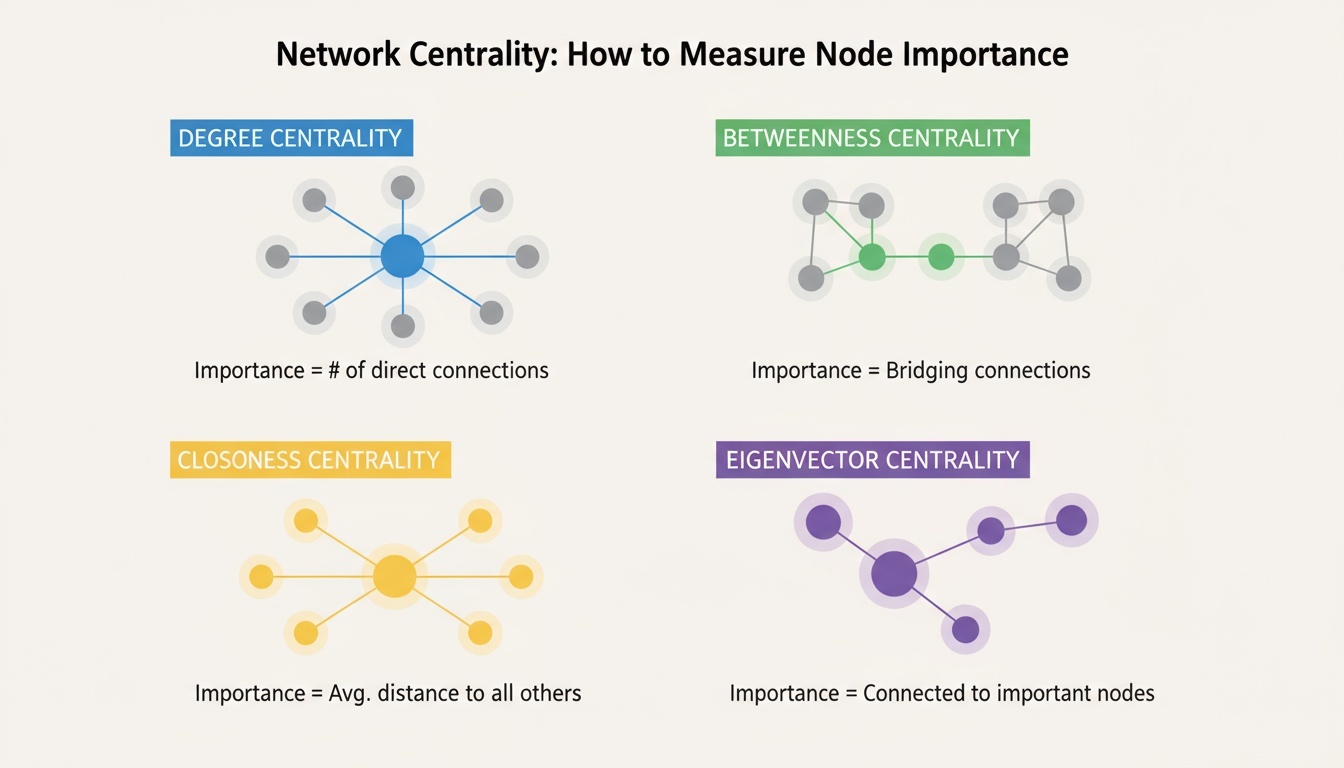
중심성 지표 비교
네트워크 분석에서 중심성(Centrality)은 노드가 네트워크 내에서 얼마나 중요한가를 수치적으로 표현한 것이다.
각 지표는 중요성을 정의하는 기준이 서로 다르며, 분석 목적에 따라 적절한 지표를 선택해야 한다.
Degree 중심성 (Degree Centrality)
-
한 노드가 얼마나 많은 엣지와 연결되어 있는지를 나타내는 가장 단순한 형태의 중심성이다.
-
연결 수가 많을수록 중심성이 높다.
-
방향 그래프의 경우에는
in-degree(들어오는 엣지 수),out-degree(나가는 엣지 수)로 구분하여 해석한다. -
예시: SNS에서 친구가 많은 사용자, 도로망에서 많은 도로와 연결된 교차로.
- 정의 수식
-
\( \deg(v) \): 노드 \( v \)의 연결 수
-
\( N \): 전체 노드 수
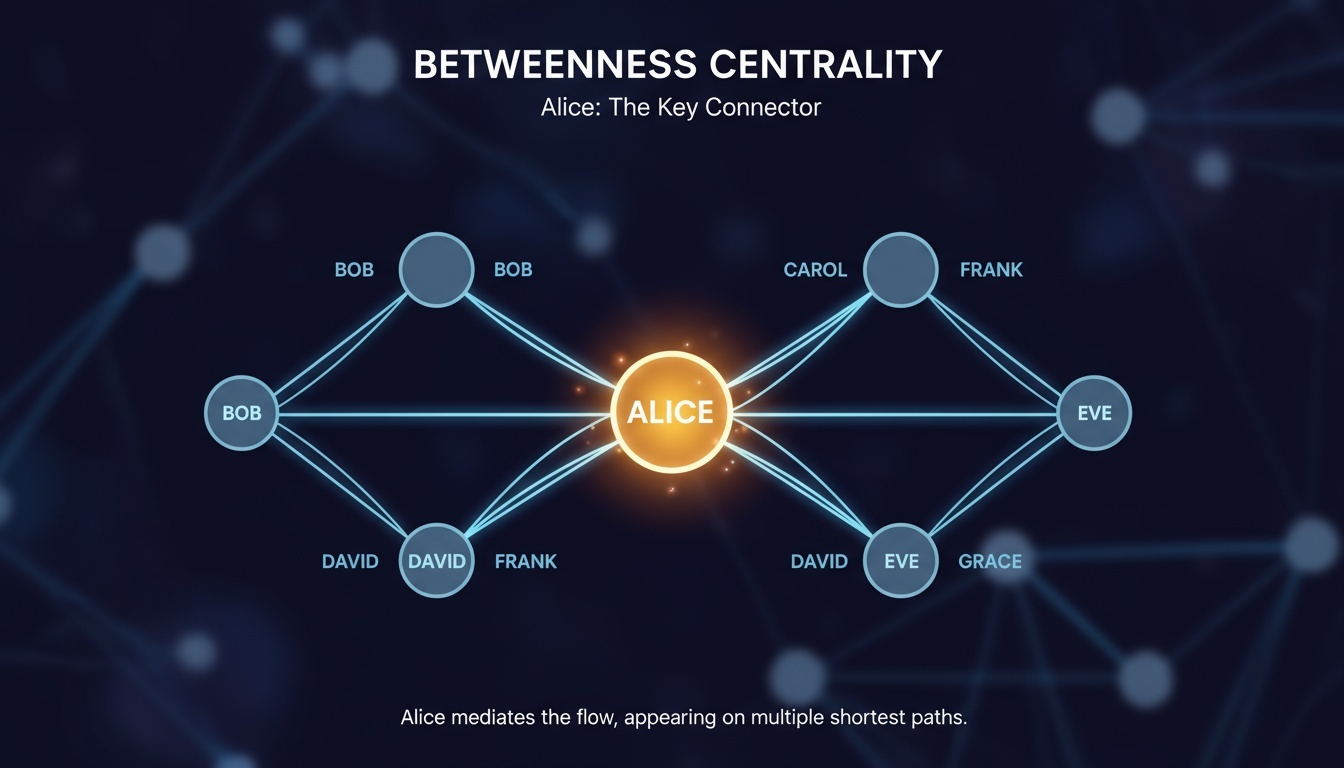
Betweenness 중심성 (Betweenness Centrality)
-
특정 노드가 다른 노드 쌍 간의 최단 경로 위에 얼마나 자주 등장하는가를 측정한다.
-
네트워크 내에서 정보나 자원의 흐름을 중개하는 역할을 하는 노드를 식별할 때 유용하다.
-
예시: 물류 네트워크의 주요 허브, 조직 내 중개 관리자.
- 정의 수식
-
\( \sigma_{st} \): 노드 \( s \)에서 \( t \)로 가는 최단 경로의 개수
-
\( \sigma_{st}(v) \): 그 경로 중 노드 \( v \)가 포함된 경로의 개수
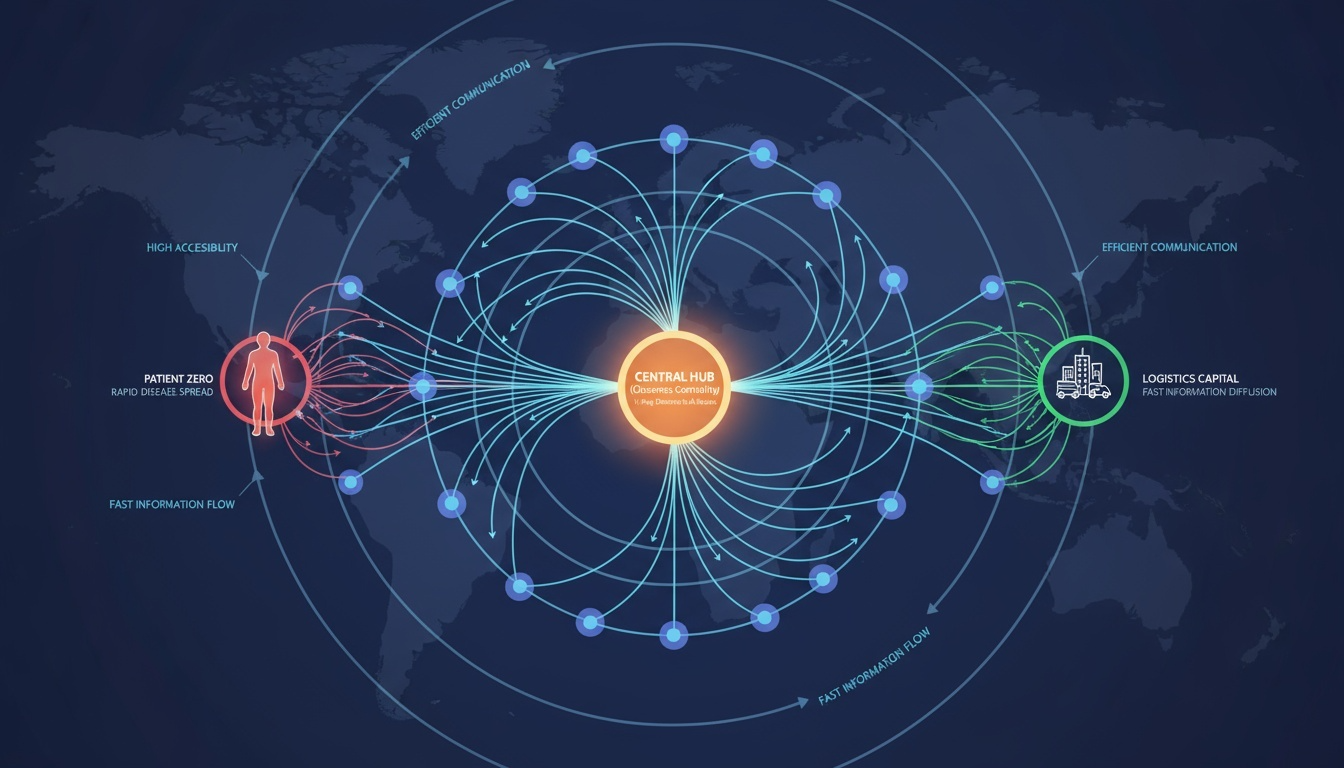
Closeness 중심성 (Closeness Centrality)
-
한 노드에서 다른 모든 노드까지의 평균 거리의 역수로 정의된다.
-
네트워크 전체와의 접근성(Accessibility) 혹은 정보 확산 속도를 나타낸다.
-
값이 높을수록 다른 노드로 빠르게 접근할 수 있다.
-
예시: 감염병 확산 네트워크에서 전염이 빠른 사람, 전국 물류망의 중심 도시.
- 정의 수식
-
\( d(v, t) \): 노드 \( v \)에서 \( t \)까지의 최단 거리
-
\( N \): 전체 노드 수
Eigenvector 중심성 (Eigenvector Centrality)
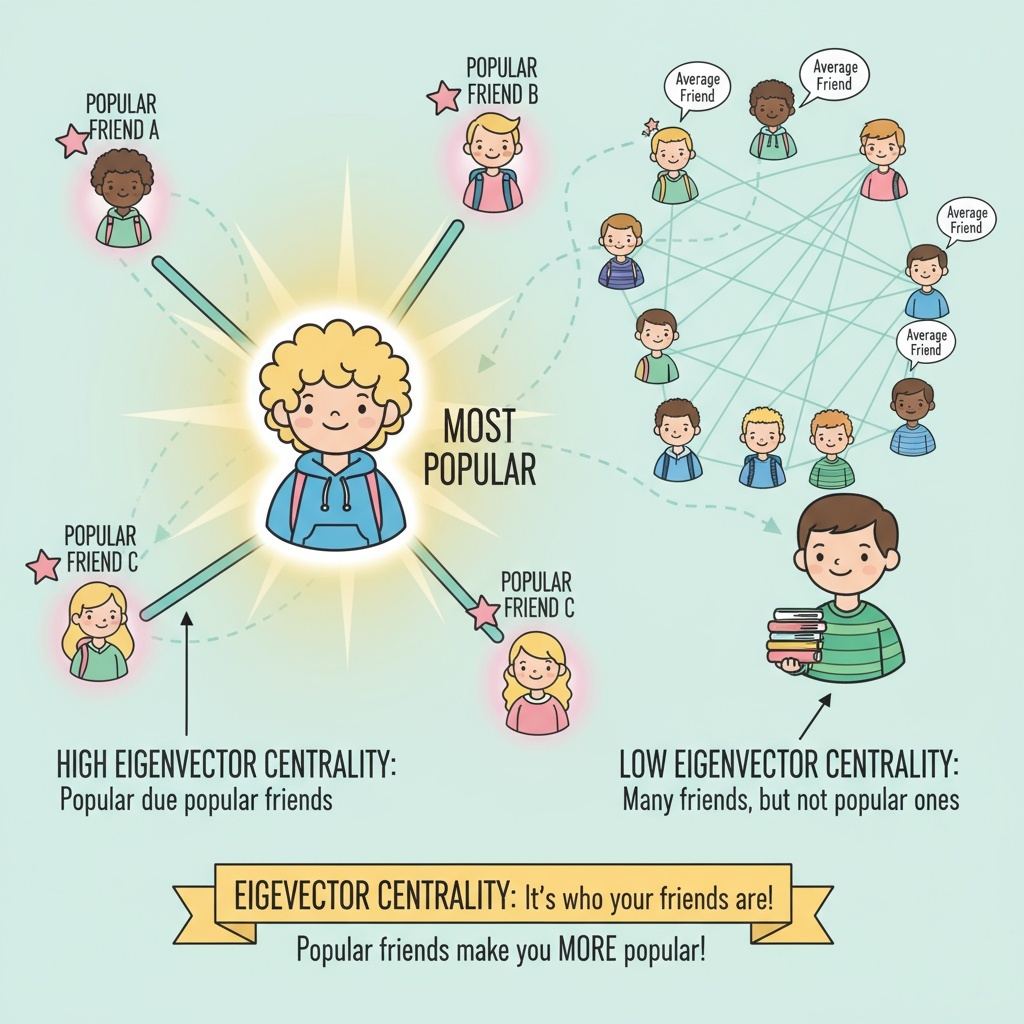
Eigenvector 중심성은 노드의 중요도가 연결된 이웃 노드의 중요도에 의해 결정된다는 아이디어를 기반으로 한다. 즉, 단순히 많이 연결된 노드가 중요한 것이 아니라, 영향력 있는 이웃과 연결된 노드가 더 중요하다는 가정이다.
이 개념은 다음과 같은 식으로 표현된다.
-
\(x_v\) : 노드 \(v\)의 중심성 값
-
\(A_{vt}\) : 인접 행렬(Adjacency Matrix)의 원소 (연결되면 1, 아니면 0)
-
\(N(v)\) : 노드 \(v\)에 연결된 이웃 노드 집합
이를 행렬 형태로 쓰면:
하지만 실제 해에서는 스케일 조정이 필요하므로 다음과 같은 고유벡터 방정식(Eigenvector Equation)이 사용된다.
Eigenvector & Eigenvalue 관련 동영상
즉, 그래프의 인접 행렬 \(A\)에 대해 해당 중심성 벡터 \(\mathbf{x}\)는 고유벡터(Eigenvector)가 되고, 그 크기를 결정하는 \(\lambda\)는 고유값(Eigenvalue)이다.
따라서 이웃 노드의 영향력까지 고려하는 중심성 지표이며, 계산 과정이 고유벡터(Eigenvector)를 구하는 것과 동일해진다.
결과적으로 중심성의 이름은 Eigenvector 중심성 이다.
Eigenvector 중심성의 특징
-
단순히 연결 수만 보는 것이 아니라, 영향력 있는 이웃 노드와 얼마나 연결되어 있는가를 함께 고려한다.
-
“영향력 있는 친구가 많을수록 영향력 있는 사람”이라는 개념이다.
-
단순 연결 수보다 연결의 질(영향력 있는 이웃) 이 중요하다는 직관이 반영된다.
-
예시:
-
학술 인용 네트워크 : 영향력 있는 연구자 탐색
-
SNS 분석 : 인플루언서 추천
-
범죄/외교 네트워크 : 핵심 인물 탐색
-

- Eigenvector를 정의하는 수식
-
\( A_{vt} \): 인접 행렬의 요소 (노드 \( v \)와 \( t \)의 연결 여부)
-
Example: 노드가 4개 있고 1–2, 2–3, 3–4만 연결되어 있다는 인접행렬 \( A_{vt} \)는 다음과 같다.
1 2 3 4 1 0 1 0 0 2 1 0 1 0 3 0 1 0 1 4 0 0 1 0 -
\( x_v \): 노드 \( v \)의 중심성 값
- 초기에는 모든 노드의 중심성 값을 동일하게 1로 설정한다.
\[ x_v^{(0)} = 1 \]- 그리고 다음과 같은 반복 갱신(Iterative Update)을 수행한다.
\[ x_v^{(k+1)} = \sum_{t \in N(v)} A_{vt} \cdot x_t^{(k)} \]-
이웃 노드의 중심성 값이 높을수록 \(x_v\)도 증가한다.
-
반복을 계속하면 중심성 값이 안정(수렴)된다.
-
\( \lambda \): 고유값(eigenvalue)
- Eigenvector 중심성의 핵심 수식은 다음과 같다.
\[ A \mathbf{x} = \lambda \mathbf{x} \]- 이를 변형하면 다음 조건을 만족해야 한다.
\[ (A - \lambda I)\mathbf{x} = 0 \]- 여기서 비자명한 해(0이 아닌 벡터)가 존재하기 위한 조건은 다음과 같다.
\[ \det(A - \lambda I) = 0 \]- 중심성 벡터는 가장 큰 고유값에 대응하는 고유벡터로 수렴하기 때문에 \(A\)의 A의 가장 큰 고유값(= 주 고유값, principal eigenvalue)을 사용한다.
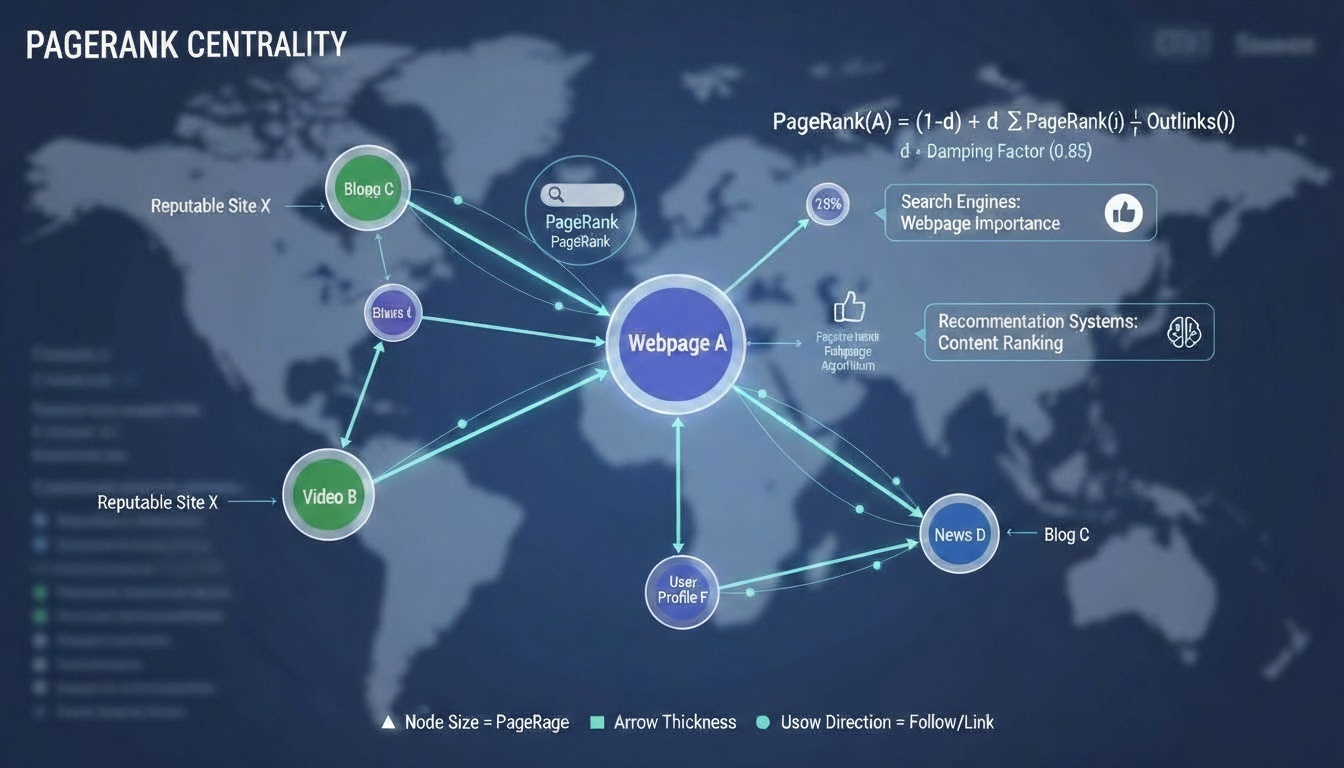
PageRank 중심성 (PageRank Centrality)
PageRank 관련 동영상
-
사용자가 링크를 따라 무작위로 이동(Random Walk) 한다고 가정하여 각 노드의 중요도를 확률적으로 계산한다.
-
단순 연결 수뿐 아니라 링크의 품질과 방향성을 함께 고려한다.
-
예시: 검색 엔진의 웹페이지 중요도 계산, 추천 시스템의 콘텐츠 순위 평가.
- 정의 수식
-
\( \alpha \): 감쇠 계수(
damping factor), 일반적으로0.85사용 -
\( M(v) \): 노드 \( v \)로 연결된 이웃 노드들의 집합 (incoming links)
-
\( L(t) \): 노드 \( t \)의 out-degree (출발 엣지 수)
-
\( N \): 전체 노드 수
요약
| 중심성 | 계산 방식 | 해석 포인트 | 활용 사례 |
|---|---|---|---|
| Degree (차수) |
특정 노드에 연결된 엣지 수 | 단순하지만 직관적인 활동성 지표 | SNS 친구 수, 도로 교차점 연결 |
| Betweenness (매개) |
최단경로 상에 등장하는 비율 | 정보 흐름을 통제하는 노드 탐색 | 물류 허브, 중개 플랫폼 |
| Closeness (근접) |
다른 노드까지의 평균 거리 역수 | 네트워크 전체와 얼마나 가까운지 | 전염 확산 속도, 서비스 커버리지 |
| Eigenvector (고유벡터) |
영향력 있는 이웃과 연결 정도 | "영향력 있는 이웃" 효과 반영 | 인플루언서 탐색, 학술 네트워크 |
| PageRank | 확률적 무작위 이동 기반 점수 | 웹 페이지 랭킹, 추천 시스템 | 검색 엔진, 콘텐츠 추천 |
중심성 계산 실습
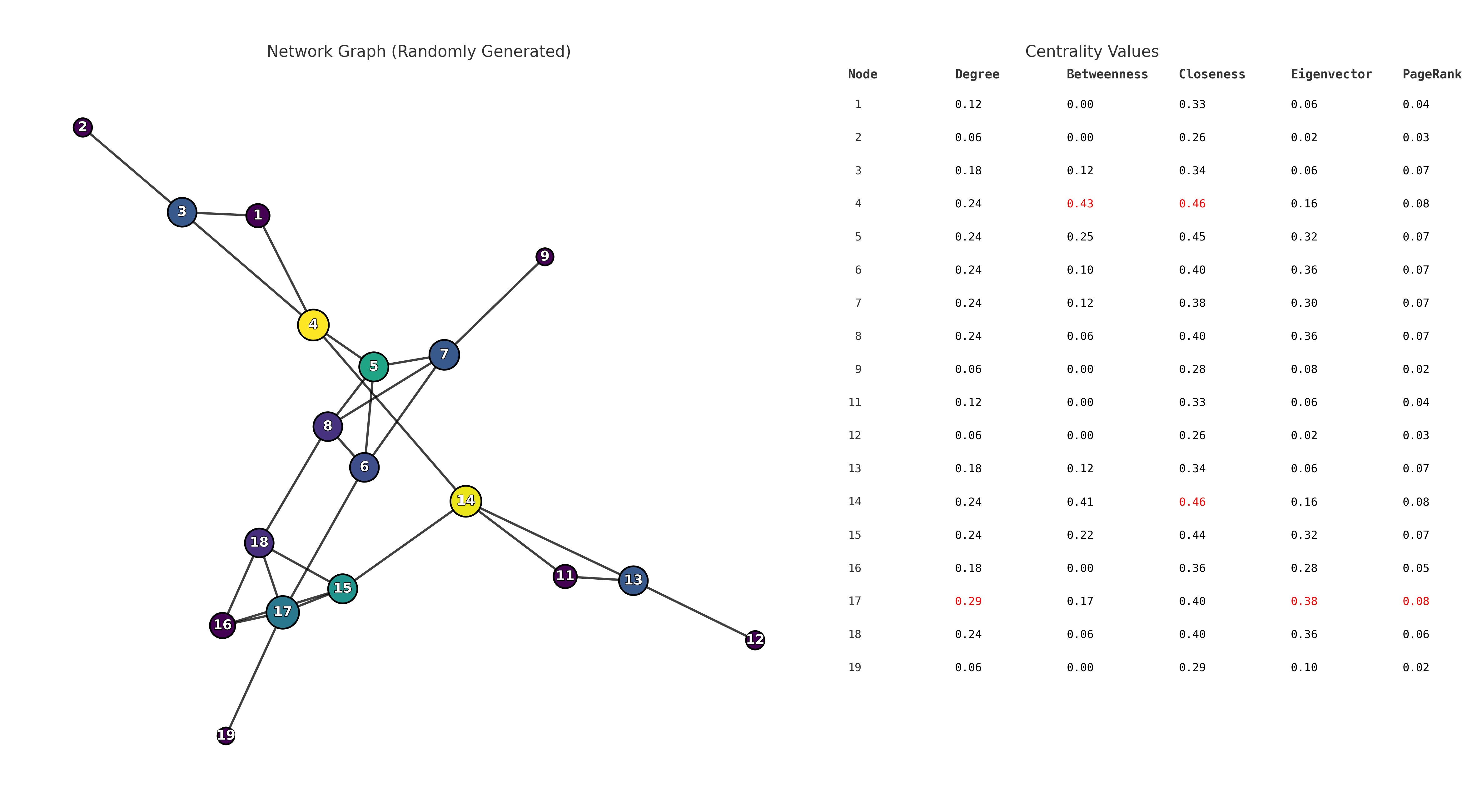
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
# 1) Base graph
G = nx.Graph()
G.add_edges_from([
(1, 3), (1, 4), (2, 3), (3, 4),
(4, 5),
(5, 6), (5, 7), (5, 8),
(6, 7), (6, 8), (7, 8),
(7, 9)
])
# 2) Augment graph: duplicate with +10 offset and add cross-edges
H = nx.Graph()
H.add_edges_from(G.edges())
H.add_edges_from([(u + 10, v + 10) for u, v in G.edges()])
G_aug = nx.compose(G, H)
G_aug.add_edges_from([(4, 14), (8, 18), (6, 17)])
# 3) Centralities
deg = nx.degree_centrality(G_aug)
bet = nx.betweenness_centrality(G_aug)
close = nx.closeness_centrality(G_aug)
eig = nx.eigenvector_centrality(G_aug, max_iter=500)
pr = nx.pagerank(G_aug, alpha=0.85)
# 4) Nodes that achieve the maximum value per centrality (for red highlight)
max_deg_nodes = [n for n, v in deg.items() if v == max(deg.values())]
max_bet_nodes = [n for n, v in bet.items() if v == max(bet.values())]
max_close_nodes = [n for n, v in close.items() if v == max(close.values())]
max_eig_nodes = [n for n, v in eig.items() if v == max(eig.values())]
max_pr_nodes = [n for n, v in pr.items() if v == max(pr.values())]
# 5) Layout
pos = nx.spring_layout(G_aug, seed=42)
# 6) Figure (no global title)
fig = plt.figure(figsize=(18, 10))
gs = fig.add_gridspec(1, 2, width_ratios=[3.2, 2.0])
ax_graph = fig.add_subplot(gs[0, 0])
ax_info = fig.add_subplot(gs[0, 1])
# 7) Draw graph
node_sizes = [pr[n] * 10000 for n in G_aug.nodes()] # larger nodes
node_colors = [bet[n] for n in G_aug.nodes()]
nx.draw_networkx_edges(G_aug, pos, ax=ax_graph, alpha=0.75, width=2.0)
nx.draw_networkx_nodes(
G_aug, pos, ax=ax_graph,
node_size=node_sizes,
node_color=node_colors,
cmap="viridis",
edgecolors="black",
linewidths=1.5
)
# 8) Node ID labels: white text with thin black outline
for n, (x, y) in pos.items():
txt = ax_graph.text(
x, y, str(n),
fontsize=12, weight="bold",
ha="center", va="center",
color="white"
)
txt.set_path_effects([
path_effects.Stroke(linewidth=1.0, foreground="black"),
path_effects.Normal()
])
# 9) Graph title (left axis), no global figure title
ax_graph.set_title("Network Graph (Randomly Generated)", fontsize=14)
ax_graph.axis("off")
# 10) Side panel (right axis)
ax_info.set_title("Centrality Values", fontsize=14)
ax_info.axis("off")
headers = ["Node", "Degree", "Betweenness", "Closeness", "Eigenvector", "PageRank"]
x_positions = [0.02, 0.23, 0.45, 0.67, 0.89, 1.11]
# Header row
for x, h in zip(x_positions, headers):
ax_info.text(x, 0.98, h, fontsize=11, fontweight="bold", family="monospace")
# Rows: nodes ascending
sorted_nodes = sorted(G_aug.nodes())
y_start, dy = 0.94, 0.045
for i, n in enumerate(sorted_nodes):
y = y_start - i * dy
if y < 0.02:
break
# Determine highlight color for each centrality column
colors = ["black"] * 5
if n in max_deg_nodes: colors[0] = "red"
if n in max_bet_nodes: colors[1] = "red"
if n in max_close_nodes: colors[2] = "red"
if n in max_eig_nodes: colors[3] = "red"
if n in max_pr_nodes: colors[4] = "red"
vals = [
f"{n:>2}",
f"{deg[n]:.2f}",
f"{bet[n]:.2f}",
f"{close[n]:.2f}",
f"{eig[n]:.2f}",
f"{pr[n]:.2f}"
]
ax_info.text(x_positions[0], y, vals[0], fontsize=10, family="monospace")
for idx, v in enumerate(vals[1:], start=1):
ax_info.text(x_positions[idx], y, v, fontsize=10, family="monospace", color=colors[idx-1])
plt.tight_layout(rect=[0, 0, 1, 0.96])
# 11) Save
plt.savefig("centrality_comparison.png", dpi=260)
plt.show()
분석 팁
-
중심성 값이 높다고 해서 항상 "좋다"고 해석할 수 있는 것은 아니다. 예를 들어 매개 중심성이 높은 노드는 정보 흐름을 제어하지만, 동시에 병목 지점일 수 있다.
-
지표 간 상관관계를 파악하면 네트워크의 구조적 특징을 더 잘 이해할 수 있다. 예: 차수 중심성과 페이지랭크가 모두 높다면 해당 노드가 영향력 있는 허브일 가능성이 높다.
중심성 시각화
중심성 값을 시각적으로 표현할 때는 다음과 같은 기법을 활용한다.
-
노드 크기를 중심성 값에 비례하도록 조정.
-
색상으로 중심성 등급(상/중/하)을 구분.
-
그래프 레이아웃을 선택(Force-directed, Circular, Geographical 등)해 정보 전달력을 높임.
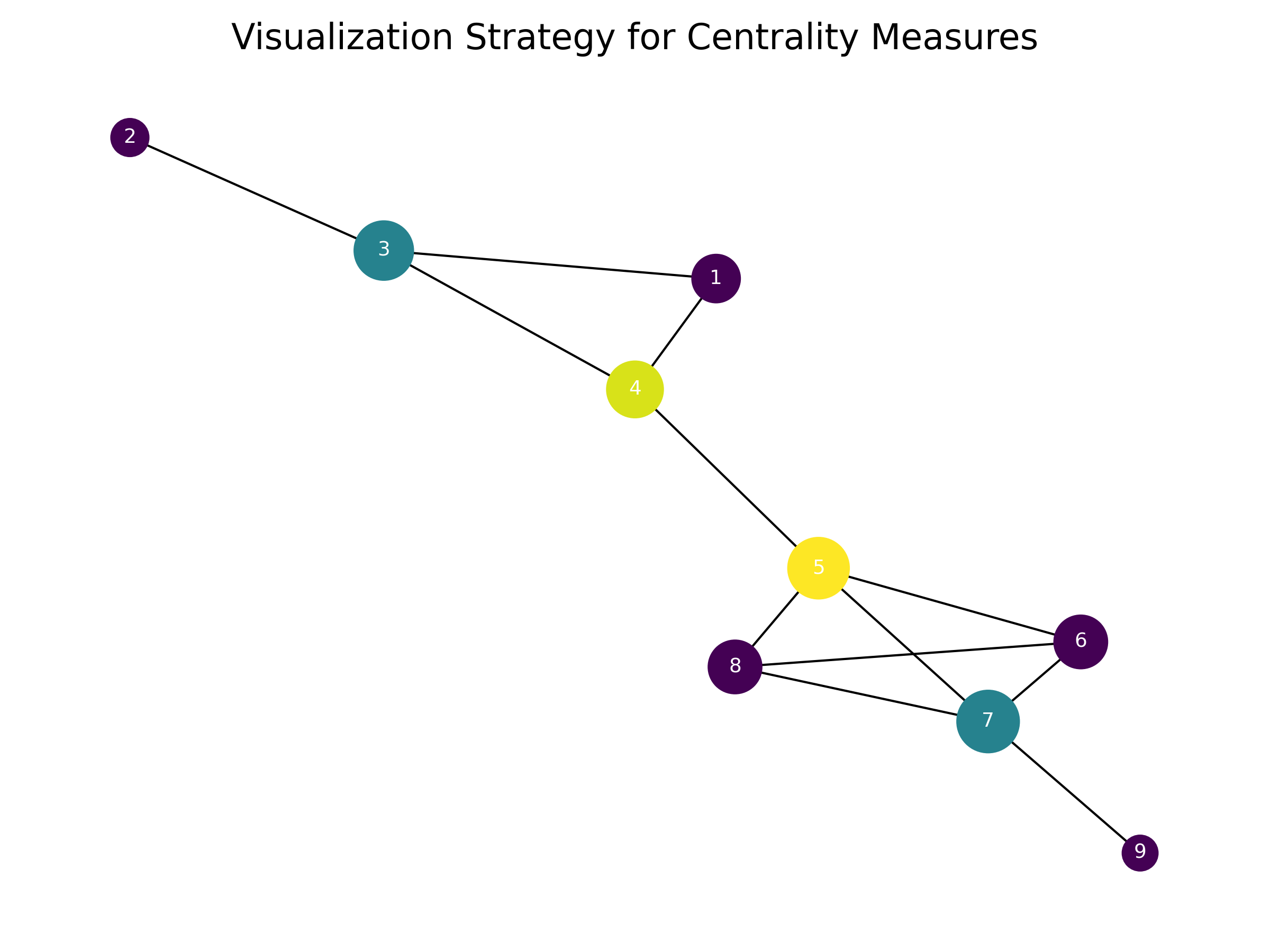
# 샘플 그래프 생성
# 중심성(PageRank, Betweenness) 계산
# PageRank로 노드 크기, Betweenness로 노드 색상 매핑
# 시각화 및 파일 저장
import matplotlib.pyplot as plt
import networkx as nx
# 1) 샘플 그래프 생성 (무방향)
G = nx.Graph()
edges = [
(1, 3), (1, 4), (2, 3), (3, 4), # cluster A
(4, 5), # bridge
(5, 6), (5, 7), (5, 8), # cluster B
(6, 7), (6, 8), (7, 8),
(7, 9) # tail
]
G.add_edges_from(edges)
# 2) 중심성 계산 (필요 지표만 계산)
centralities = {
"pagerank": nx.pagerank(G, alpha=0.85),
"betweenness": nx.betweenness_centrality(G, normalized=True),
}
# 3) 레이아웃 및 시각화 매핑
plt.figure(figsize=(8, 6))
pos = nx.spring_layout(G, seed=42)
# PageRank -> 노드 크기, Betweenness -> 노드 색
sizes = [centralities["pagerank"][node] * 5_000 for node in G.nodes()]
colors = [centralities["betweenness"][node] for node in G.nodes()]
# 4) 그래프 그리기
nx.draw_networkx(
G,
pos=pos,
node_size=sizes,
node_color=colors,
cmap="viridis",
with_labels=True, # 노드 번호 라벨
font_size=9,
font_color="white", # 어두운 색 노드에서도 보이도록
)
plt.title("Visualization Strategy for Centrality Measures", fontsize=16)
plt.axis("off")
plt.tight_layout()
# 5) 저장 및 표시
plt.savefig("centrality_visualization_strategy.png", dpi=300)
plt.show()
네트워크 시각화 전략
네트워크 시각화 전략 비교
| 시각화 유형 | 장점 | 단점 | 주요 도구 |
|---|---|---|---|
| 정적 시각화 | 보고서나 논문에 삽입하기 용이함 기본 구조를 빠르게 전달 가능 |
복잡한 네트워크의 세부 관계 파악이 어려움 | matplotlib, seaborn, geopandas, ggplot |
| 인터랙티브 시각화 | 노드 상세 정보 조회 가능 확대/축소 등 탐색적 분석 가능 |
배포 환경에 따라 성능 및 호환성 고려 필요 | pyvis, plotly, bokeh, kepler.gl, Gephi |
정적 시각화
-
장점: 보고서나 논문에 삽입하기 쉽고, 기본적인 구조를 빠르게 전달할 수 있다.
-
단점: 복잡한 네트워크의 세부 관계를 파악하기 어렵다.
-
도구:
matplotlib,seaborn,geopandas,ggplot.
인터랙티브 시각화
필요한 패키지 설치
-
장점: 노드에 마우스를 올리면 상세 속성이 나타나고, 확대/축소가 가능하다.
-
단점: 배포 환경(웹/노트북)에 따라 성능과 호환성 고려가 필요하다.
-
도구:
pyvis,plotly,bokeh,kepler.gl,Gephi.
인터렉티브 시각화 결과: 아래 코드를 실행한 결과 (html)
- 결과 파일(
.html) 직접 다운로드: Click me
pyvis 패키지 소개
pyvis는 networkx 그래프를 몇 줄의 코드만으로 vis.js 기반 인터랙티브 HTML로 변환해 주는 경량 라이브러리다.
노드에 마우스를 올려 속성을 Tooltip으로 확인하고, 드래그·확대·축소 같은 인터랙션을 기본 제공하므로 탐색 중심 EDA와 공유용 리포트 제작에 유용하다.
-
NetworkX 친화성:
Network객체에add_node,add_edge만 호출하면networkx에서 계산한 중심성·커뮤니티 정보를 그대로 시각화에 반영할 수 있다. -
설정 난이도↓:
set_options에 vis.js JSON 옵션을 넘겨 물리 시뮬레이션 레이아웃, 색상, 라벨링 전략을 직관적으로 맞출 수 있다. -
오프라인 배포:
cdn_resources="in_line"을 지정하면 외부 CDN 없이 단일 HTML 파일이 생성되어 방화벽/문서 첨부 환경에서도 문제없이 열 수 있다. -
웹 임베딩 용이: 생성된 HTML은 Flask/Django 템플릿, Streamlit 컴포넌트, Jupyter iframe 등 어디든 삽입 가능해 데모 공유가 간편하다.
TIP: 노드 크기·색상을 중심성, 커뮤니티 등 핵심 지표와 연결하면 사용자가 직접 그래프를 조작하며 빠르게 패턴을 파악할 수 있다.
[참고] 자바스크립트 패키지 vis.js 소개
-
역할: 그래프·타임라인·네트워크 등 동적 시각화를 지원하는 오픈소스 JS 라이브러리로 PyVis가 내부적으로 활용한다.
-
렌더링 엔진: HTML
<canvas>기반 force-directed 레이아웃으로 수백~수천 노드를 부드럽게 배치한다. -
상호작용: 줌/팬, 다중 선택, Tooltip, 물리 엔진 토글 등 사용자 조작 기능이 기본 내장돼 있다.
-
커스터마이징: JSON 옵션으로 노드/엣지 스타일, 물리 파라미터, 이벤트 핸들러를 세밀하게 제어할 수 있다.
-
생태계: PyVis 외에도 React/Vue 대시보드나 순수 JS 프로젝트에 직접 포함해 사용할 수 있다.
-
자료: vis.js 공식 문서에서 모듈별 API와 Playground를 제공한다.
물리 엔진 토글:
physics.enabled옵션이나 PyVis의toggle_physics()함수로 force-directed 시뮬레이션을 켜고 끌 수 있다.ON이면 노드가 중력/탄성 규칙에 따라 움직이며 레이아웃을 찾고,OFF면 해당 위치를 고정한 정적 배치로 볼 수 있다.
pip install networkx pyvis
# interactive_network_3x_exact_fixed.py
# - 단일 그래프에서 노드/엣지 수를 정확히 3배(노드=27, 엣지=36)
# - 중심성 계산 후 pyvis로 인터랙티브 HTML 생성
# - cdn_resources='in_line' 으로 오프라인/방화벽 환경에서도 표시 보장
"""
실습 흐름 가이드
1. PyVis/NetworkX를 불러온 뒤 기본 그래프를 정의한다.
2. 목표 노드·엣지 수에 맞춰 허브 노드를 중심으로 네트워크를 확장한다.
3. 핵심 중심성 지표(PageRank, Betweenness 등)를 계산하고 시각화 매핑용 값을 만든다.
4. PyVis `Network` 객체를 생성해 물리 엔진 옵션, 노드/엣지 스타일을 설정한다.
5. 노드/엣지를 PyVis에 주입하면서 Tooltip, 크기, 색상을 지표와 연결한다.
6. 최종 HTML을 생성·저장하여 브라우저나 리포트에 임베딩한다.
"""
from pyvis.network import Network # vis.js 기반 인터랙티브 그래프 생성기
import networkx as nx # 그래프 생성·분석 도구
import math # 노드 크기 스케일링에 사용
# 0) Base graph (nodes=9, edges=12) -------------------------------------------
base_edges = [
(1, 3), (1, 4), (2, 3), (3, 4),
(4, 5),
(5, 6), (5, 7), (5, 8),
(6, 7), (7, 8),
(7, 9)
]
G = nx.Graph() # 무방향 그래프 객체 생성
G.add_edges_from(base_edges) # 엣지 리스트를 통해 기본 구조 입력
TARGET_NODES = 27 # 최종 목표 노드 수
TARGET_EDGES = 36 # 최종 목표 엣지 수
# 1) 노드 개수 채우기 (10..27 추가) + 허브(5)와 연결 -------------------------
current_max = max(G.nodes) # 현재 그래프의 최대 노드 번호
for new_n in range(current_max + 1, TARGET_NODES + 1):
G.add_node(new_n) # 새 노드 추가
G.add_edge(5, new_n) # 허브(5)에 연결해 단일 컴포넌트 유지
assert len(G.nodes) == 27, f"nodes={len(G.nodes)} (expect 27)"
# 2) 엣지 수 맞추기 -----------------------------------------------------------
# - 실습 목표(노드=27, 엣지=36)에 맞춰 정해진 규모를 확보해야
# 이후 중심성 비교나 시각화가 동일 조건에서 재현 가능하다.
# - 고르게 분포된 추가 엣지를 넣어 그래프가 너무 희박해지지 않도록 한다.
needed = TARGET_EDGES - G.number_of_edges() # 추가로 필요한 엣지 개수
extra_pairs = [
(6, 10), (7, 11), (8, 12),
(15, 16), (20, 21), (22, 23),
(24, 25), (26, 27) # 여유 후보
]
added = 0 # 실제로 추가된 엣지 카운터
for u, v in extra_pairs:
if added >= needed:
break # 목표 수를 채우면 조기 종료
if u in G and v in G and not G.has_edge(u, v):
G.add_edge(u, v) # 존재하는 노드 쌍만 연결
added += 1 # 새 엣지를 추가했음을 기록
assert G.number_of_edges() == 36, f"edges={G.number_of_edges()} (expect 36)"
# 3) 중심성 계산 --------------------------------------------------------------
deg = nx.degree_centrality(G) # 연결 수 기반 중요도
bet = nx.betweenness_centrality(G, normalized=True) # 경로 중개 빈도
close = nx.closeness_centrality(G) # 평균 거리 역수
eig = nx.eigenvector_centrality(G, max_iter=500) # 영향력 높은 이웃과의 연결
pr = nx.pagerank(G, alpha=0.85) # PageRank 확률 분포
"""
중심성 값 활용 팁
- Degree: 연결 허브를 찾는 지표. 보고서에서는 상위 노드를 표로 정리하거나 굵은 테두리로 강조하기 좋다.
- Betweenness: 여러 노드가 거쳐 가는 중개자를 알려주므로 색상(아래 bet_to_hex)으로 매핑해 구조적 브리지를 시각적으로 드러낸다.
- Closeness: 전체를 빠르게 탐색할 수 있는 노드를 보여주니 Tooltip에 포함해 “접근성이 높은 노드”를 설명한다.
- Eigenvector: 영향력 있는 이웃과 연결 여부를 나타내므로 상위 노드를 필터링하거나 추천 후보를 고를 때 활용한다.
- PageRank: 이 스크립트에서는 `scale_pr` 함수에 들어가 PyVis 노드 크기를 결정한다. 확률이 높은 노드일수록 화면에서 크게 보이도록 설정.
"""
# 4) 색상 매핑 (Betweenness → 색) --------------------------------------------
# - betweenness 값이 높을수록 밝은/따뜻한 색으로 보여 중개자가 눈에 띄도록 한다.
# - matplotlib이 설치돼 있으면 Viridis 컬러맵을 사용하고, 설치돼 있지 않은 환경을 대비해
# try/except로 수동 색상 팔레트(보라→노랑)를 준비해 둔다.
try:
import matplotlib.cm as cm
import matplotlib.colors as mcolors
def bet_to_hex(betweenness_value: float) -> str:
norm = mcolors.Normalize(vmin=0, vmax=1) # 0~1 구간으로 정규화
return mcolors.to_hex(cm.viridis(norm(betweenness_value))) # viridis 색상표 사용
except Exception:
# (Fallback) matplotlib 미설치 또는 노트북 환경 문제 시에도 실행이 끊기지 않도록
# 미리 정의한 다섯 단계 색상을 사용한다.
def bet_to_hex(betweenness_value: float) -> str:
if betweenness_value < 0.2: return "#440154"
if betweenness_value < 0.4: return "#31688e"
if betweenness_value < 0.6: return "#35b779"
if betweenness_value < 0.8: return "#fde725"
return "#ffcc00"
# 5) pyvis 네트워크 구성 (중요: cdn_resources='in_line') ----------------------
net = Network(
height="650px",
width="100%",
notebook=False,
directed=False,
bgcolor="#ffffff",
font_color="#222222",
cdn_resources="in_line" # 외부 CDN 없이 HTML 하나로 동작하게 설정
)
# vis.js 옵션(JSON)으로 물리 엔진·인터랙션 세부 설정
# - interaction.hover: 노드 위로 마우스를 가져가면 Tooltip 표시
# - interaction.navigationButtons: 확대/축소, 중앙 정렬 버튼 UI 제공
# - interaction.multiselect: 드래그로 여러 노드를 동시에 선택 가능
# - physics.enabled: 물리 레이아웃 활성화 여부
# - physics.stabilization: 레이아웃 안정화 반복 횟수 (흔들림을 줄이기 위함)
# - physics.barnesHut: force-directed 파라미터(중력, 스프링 길이·강도, 감쇠 비율)
# - nodes.borderWidth / shadow: 노드 테두리 두께와 그림자 여부
# - edges.smooth: 엣지를 곡선으로 표현해 겹침을 줄임
# - edges.color.opacity: 엣지 투명도 조절로 배경 대비 확보
net.set_options("""
{
"interaction": {
"hover": true,
"navigationButtons": true,
"multiselect": true
},
"physics": {
"enabled": true,
"stabilization": {
"enabled": true,
"iterations": 400
},
"barnesHut": {
"gravitationalConstant": -25000,
"centralGravity": 0.3,
"springLength": 120,
"springConstant": 0.02,
"damping": 0.09
}
},
"nodes": {
"borderWidth": 1,
"shadow": true
},
"edges": {
"smooth": {
"type": "dynamic",
"roundness": 0.4
},
"color": {
"opacity": 0.7
}
}
}
""")
# 6) (핵심) 그래프를 pyvis에 실제로 추가 --------------------------------------
# 1) PageRank 값을 노드 크기로 변환할 스케일 함수 정의
# 2) 각 노드에 Tooltip/크기/색상/레이블을 부여하며 PyVis에 add_node
# 3) 모든 엣지를 add_edge로 연결해 PyVis 그래프를 완성
pagerank_values = list(pr.values()) # 노드 크기 스케일링을 위한 값
pagerank_min, pagerank_max = min(pagerank_values), max(pagerank_values)
def scale_pagerank_to_size(
pagerank_value: float,
min_size_px: int = 12,
max_size_px: int = 42
) -> float:
"""
PageRank 확률(0~1)을 시각적으로 구분 가능한 픽셀 크기로 변환한다.
- 중심성이 모두 같으면 중간 크기를 고정으로 반환해 레이아웃 붕괴를 방지한다.
- 그렇지 않으면 선형 보간법으로 최소/최대 크기 사이 값을 돌려준다.
"""
if math.isclose(pagerank_max, pagerank_min):
return (min_size_px + max_size_px) / 2 # 모든 값이 같으면 평균 크기
normalized = (pagerank_value - pagerank_min) / (pagerank_max - pagerank_min)
return min_size_px + normalized * (max_size_px - min_size_px) # 원하는 픽셀 범위에 매핑
# 각 노드를 순회하며 PyVis 그래프에 속성 정보를 포함해 추가
# PyVis에서는 node `title` 속성이 HTML Tooltip으로 노출되므로,
# 브라우저에서 결과 HTML을 열고
# 노드 위에 마우스를 올리면 중심성 지표가 바로 확인된다.
# size/color 속성은 시각적 강조에 즉시 반영된다.
for node_id in G.nodes():
title = (
f"<b>Node {node_id}</b><br>"
f"Degree: {deg[node_id]:.3f}<br>"
f"Betweenness: {bet[node_id]:.3f}<br>"
f"Closeness: {close[node_id]:.3f}<br>"
f"Eigenvector: {eig[node_id]:.3f}<br>"
f"PageRank: {pr[node_id]:.5f}"
)
# 전략:
# label은 읽기 쉬운 문자열,
# title에는 상세 지표를 HTML로,
# size/color는 중심성에 따라 동적으로 매핑
net.add_node(
node_id,
label=str(node_id),
title=title, # 마우스오버 시 표시할 중심성 정보
size=scale_pagerank_to_size(pr[node_id]), # PageRank 기반 노드 크기
color=bet_to_hex(bet[node_id]), # Betweenness 기반 색상
borderWidth=1
)
for source_node, target_node in G.edges():
net.add_edge(source_node, target_node) # 노드 간 연결선을 pyvis에 주입
# 7) HTML 생성 (브라우저 자동 열기 X) -----------------------------------------
out_path = "interactive_network.html" # 결과 파일 경로
# 7-1) pyvis가 만든 HTML 문자열 생성
html = net.generate_html(notebook=False) # cdn_resources='in_line' 설정 유지한 상태여야 함
# 7-2) UTF-8로 직접 저장
with open(out_path, "w", encoding="utf-8") as f:
f.write(html)
print(f"Saved: {out_path}")
시각화 체크리스트
-
레이아웃 선택 Force-directed 레이아웃은 관계 중심, 지리적 레이아웃은 위치 정보를 강조한다.
-
스타일 설정 노드/엣지 색상과 크기는 분석 메시지를 전달하기 위한 도구다. 중심성, 커뮤니티, 카테고리 등 어떤 정보를 강조할지를 먼저 정의한다.
-
라벨링 모든 노드에 라벨을 붙이면 오히려 가독성이 떨어지므로, 상위 노드만 라벨링하거나 토글 기능을 제공한다.
-
인터랙션 힌트 인터랙티브 시각화에서는 사용자에게 어떤 조작이 가능한지 안내 문구를 제공한다.
커뮤니티 탐지와 서브네트워크
네트워크 분석에서 자주 등장하는 질문은 "이 네트워크는 몇 개의 집단으로 나뉘는가?"이다.
-
대표적인 커뮤니티 탐지 알고리즘:
networkx.community -
다양한 그래프 데이터셋: 스탠포드 대학 (Large Network Dataset Collection)
커뮤니티 결과는 시각화와 결합해 각 집단의 특징을 설명하는 데 활용한다.
예를 들어, Louvain 알고리즘으로 나눈 커뮤니티별 평균 중심성을 비교하면 그룹 간 영향력 차이를 확인할 수 있다.
커뮤니티 탐지 실습
pip install python-louvain
import networkx as nx
import community.community_louvain as community_louvain
import matplotlib.pyplot as plt
# 1. 예제 그래프 생성
G = nx.karate_club_graph()
# 2. Louvain 알고리즘 적용 (노드:커뮤니티ID 딕셔너리 반환)
partition = community_louvain.best_partition(G)
# 3. 커뮤니티별 노드 그룹화
communities = {}
for node, comm_id in partition.items():
communities.setdefault(comm_id, []).append(node)
# 4. 커뮤니티 출력
print("\n=== Community Sub-Networks ===")
for comm_id, nodes in communities.items():
print(f"Community {comm_id}: {nodes}")
# 5. 시각화 (커뮤니티별 색상)
colors = [partition[node] for node in G.nodes()]
plt.figure(figsize=(6, 5))
nx.draw_networkx(G, node_color=colors, with_labels=True, cmap='Set3')
plt.title("Community Detection with Sub-Network Listing")
plt.show()
# plt.savefig("community_detection_subnetworks.png")
Community 0: [0, 1, 2, 3, 7, 11, 12, 13, 17, 19, 21]
Community 1: [24, 25, 28, 31]
Community 2: [4, 5, 6, 10, 16]
Community 3: [8, 9, 14, 15, 18, 20, 22, 23, 26, 27, 29, 30, 32, 33]
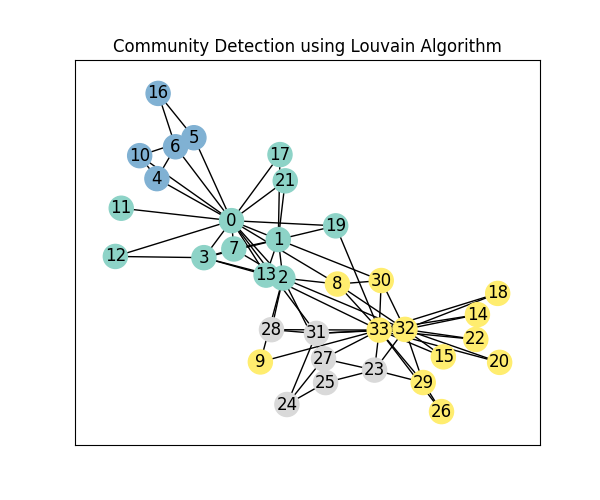
실습해볼 만한 주제 (Topics)
실습 1: 소셜 네트워크 분석
-
데이터: 동아리 활동 로그 또는 SNS 친구 목록(익명화).
-
목표:
-
엣지 리스트를 그래프로 변환하고 기본 통계(노드 수, 엣지 수, 평균 차수)를 계산한다.
-
중심성 지표 3가지 이상을 계산하여 상위 10개 노드를 도출한다.
-
커뮤니티 탐지 결과를 시각화하고, 그룹별 특징을 정리한다.
-
실습 2: 교통 네트워크 분석
-
데이터: 도시별 버스/지하철 노선, 물류 창고 간 이동 경로 등.
-
목표:
-
이동 경로 데이터를 방향 그래프로 구성하고, 경로 가중치를 설정한다.
-
혼잡도(매개 중심성)와 접근성(근접 중심성)이 높은 노드를 비교 분석한다.
-
인터랙티브 시각화로 경로 탐색 시나리오를 설명한다.
-
Home Works (with SNAP Dataset)
- 필요한 패키지 설치
pip install networkx python-louvain pyvis matplotlib pandas
- 데이터: SNAP 네트워크 데이터셋 중 한 개를 선택하여 분석하라.
| 데이터셋 | 설명 | 다운로드 | 페이지 방문 |
|---|---|---|---|
| ego-Facebook | Facebook 친구 관계 네트워크 | facebook_combined.txt.gz | Click |
| com-DBLP | 연구자 공저 네트워크 (Co-authorship) |
com-dblp.top5000.cmty.txt.gz | Click |
| Email-EU-core | 유럽 연구 기관 내부 이메일 네트워크 |
email-Eu-core.txt.gz | Click |
- 분석 목표: 선택한 네트워크에서 핵심 노드(허브)를 식별하고, 커뮤니티 구조를 시각화하여 인사이트를 도출한다.
수행 과제
-
데이터 로딩 및 그래프 구성 선택한 데이터셋을 이용해 네트워크(Graph)를 구성하고, 방향/무방향, 가중치(있을 경우) 반영 여부를 명시하라.
-
중심성 분석
-
다음 중심성 지표를 계산하고 상위 10개 노드를 표로 비교하라.
-
Degree Centrality
-
PageRank
-
(선택) Betweenness 또는 Eigenvector Centrality
-
-
커뮤니티 탐지 및 시각화
-
Louvain 알고리즘으로 커뮤니티를 탐지하고 커뮤니티별 색상 구분 시각화를 수행하라.
-
커뮤니티 수, 각 커뮤니티의 노드 수를 보고하고 주요 커뮤니티의 특성을 간략히 기술하라.
-
-
부분 네트워크(Ego-Network) 분석
-
중심성이 높은 상위 3~5개 핵심 노드를 선정하고, 각 노드의 이웃 subgraph를 추출하여
.png로 저장하라. -
각 subgraph에서 핵심 노드의 역할과 주변 구조를 간단히 해석하라.
-
-
제출물
-
분석 내용 정리 Jupyter Notebook:
week10_homework.ipynb -
생성한 시각화 이미지 및 PDF 파일
-
(선택) Pyvis 기반 인터랙티브 시각화 HTML 제출 시 가산점
-
팁
-
권장 라이브러리:
networkx,community-louvain,pyvis,matplotlib,pandas -
노트북 상단에 사용한 데이터셋명/버전, 분석 환경(파이썬/OS), 라이브러리 버전을 기록하라.
Solution
-
가능한 솔루션을 제공합니다. 가급적이면 솔루션 없이 구현해 볼 것을 추천합니다.
-
가능한 솔루션 1. 파이썬 스크립트: hw10_solution.py
-
가능한 솔루션 2. 주피터 노트북 파일: hw10_solution.ipynb
-
출력물(제출물): hw10_outputs.zip
-