시계열 분석 (Time Series Analysis)
- 강의 자료 다운로드: click me
데이터가 시간 축을 따라 관측되는 경우, 단순히 관측값만을 비교하는 것보다 시간에 따른 패턴을 이해하는 일이 중요하다.
시계열(time series) 데이터 분석은 추세(Trend), 계절성(Seasonality), 주기성(Cycle)과 같은 요소를 분해해 데이터의 구조를 파악하고, 이를 바탕으로 미래 값을 예측하거나 이상 징후를 감지하는 데 활용된다.
이번 섹션에서는 시계열 데이터의 기본 개념부터 대표적 모델링 기법(ARIMA 계열)까지 단계별로 학습한다.
학습 목표
-
시계열 데이터의 구조적 특성과 구성 요소(추세, 계절성, 불규칙성)를 설명할 수 있다.
-
시계열 분해, 정규화, 차분(differencing) 등의 전처리 기법을 실습할 수 있다.
-
정상성(stationarity) 개념과 단위근 검정(ADF test)을 이해하고 적용할 수 있다.
-
ARIMA/SARIMA 모델과 Prophet 등 대표적인 예측 기법의 구조와 사용법을 습득한다.
-
예측 결과를 평가하고 시각화하여 실무 의사결정에 활용할 수 있다.
Check Point: 주어진 시계열 데이터셋에 대해 분해, 모델링, 예측, 평가를 일련의 파이프라인으로 구현할 수 있는가?
시계열 데이터 이해하기
시계열의 정의와 특징

-
시간 순서 유지
시계열 데이터는 일정한 시간 간격으로 순차적으로 기록된 관측값의 집합이다.
한 은행의 월별 신규 계좌 수처럼 시간 흐름에 따라 쌓이는 값은 순서를 뒤섞으면 계절적 패턴을 잃어버리므로 시간 축을 보존하는 것이 무엇보다 중요하다.
-
자기상관
자기상관 또한 시계열의 대표적 특징이다. 오늘의 전력 사용량이 어제와 유사한 형태를 보이는 것처럼 인접한 시점 사이에는 날씨·요일 등 반복되는 요인이 연속적으로 영향을 준다.
동시에 스타트업의 월 매출처럼 시간이 지날수록 평균이나 분산이 달라지는 비정상성도 자주 나타나 단순 요약 통계만으로는 전체 구조를 설명하기 어렵다.
데이터사이언스에서는 이러한 특성을 먼저 파악한 뒤 분석 목적에 맞는 전처리와 모델을 선택한다. 자기상관이 강하면 일반 회귀 대신 ARIMA 등 시계열 전용 모델을 고려하고, 비정상성이 감지되면 차분이나 로그 변환으로 안정화한다.

새로운 관측이 들어올 때마다 모델을 갱신하거나 온라인 학습 기법을 활용하는 전략도 중요하다. 결국 시계열은 단순 표 형태의 데이터가 아니라 시간 축과 함께 해석해야 하는 구조적 데이터라는 점을 잊지 말아야 한다.
구성 요소
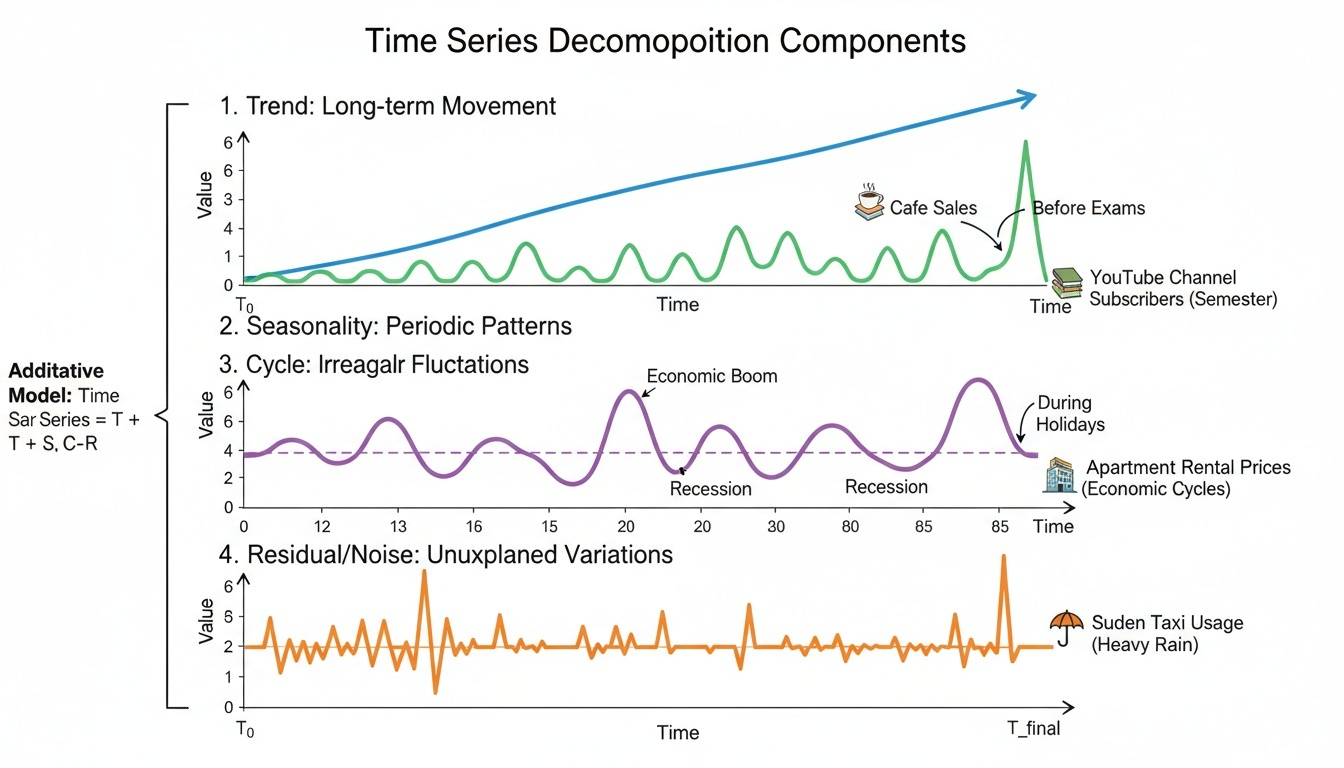
시계열을 이해할 때는 전체 관측값을 몇 가지 기본 요소로 나누어 생각하면 훨씬 쉽다. 아래 예시는 대학생에게 익숙한 생활 데이터를 기반으로 한다.
-
Trend(추세): 데이터가 오랜 기간에 걸쳐 꾸준히 상승하거나 하락하는 흐름이다.
-
예: 인기 유튜브 채널 구독자 수가 학기 내내 조금씩 증가하는 모습.
-
추세가 있으면 단순 평균보다 최근 흐름을 강조하는 분석이 필요하다.
-
-
Seasonality(계절성): 일정한 간격으로 반복되는 규칙적인 패턴이다.
-
예: 카페 매출이 시험 기간 직전에 급증했다가 방학 중에는 줄어드는 패턴.
-
계절성이 강하면 주기를 고려한 차분이나 SARIMA처럼 계절형 모델이 필요하다.
-
-
Cycle(주기성): 계절성보다 더 긴, 불규칙한 주기로 반복되는 큰 변동이다.
-
예: 경제 상황에 따라 대학 근처 원룸 임대료가 몇 년 주기로 오르내리는 현상.
-
경기 순환 등 외부 환경 변화와 깊게 연결되므로 거시 지표를 함께 살펴야 한다.
-
-
Residual/Noise(불규칙): 추세·계절성·주기로 설명되지 않는 일시적 변동이다.
-
예: 갑작스러운 폭우로 하루 동안 택시 이용량이 급증하는 상황.
-
노이즈는 완전히 제거할 수는 없지만, 이상치 탐지나 스무딩 기법으로 영향력을 줄인다.
-
아래 그림은 시계열을 네 가지 요소로 분해했을 때의 전형적인 모습을 보여준다.
데이터 준비와 탐색
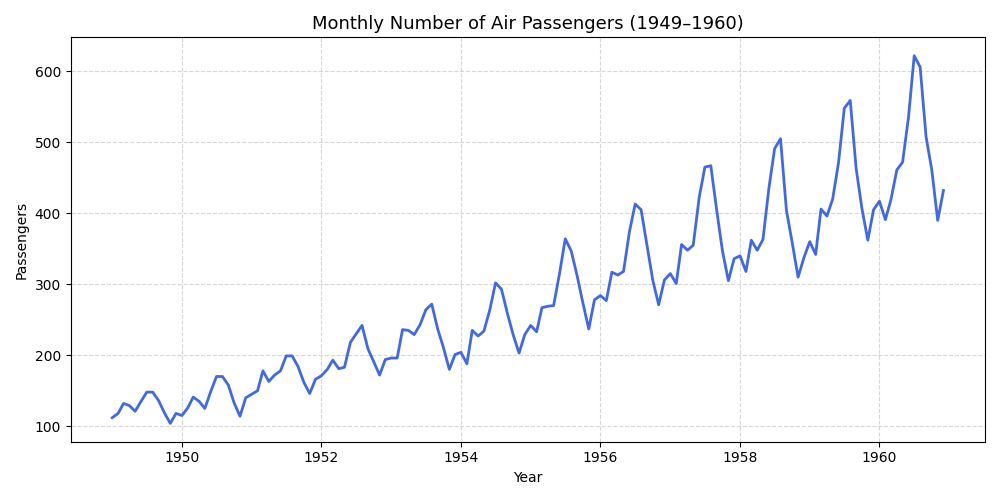
AirPassengers 데이터는 1949년부터 1960년까지의 국제선 여객 수를 월별로 기록해 장기 추세와 뚜렷한 계절성을 동시에 관찰할 수 있는 대표적인 예제다.
시계열 전처리에서 자주 마주치는 과제(누락된 월, 문자열 형태의 날짜, 시간대 미지정 등)를 한 번에 연습할 수 있다는 점에서 첫 실습용으로 적합하다.
-
실습 데이터: https://www.kaggle.com/datasets/rakannimer/air-passengers
-
직접 다운로드: click me
시계열(Time Series) 분석은 단순히 날짜가 포함된 데이터를 다루는 것이 아니라, 시간의 흐름에 따라 규칙적으로 발생하는 데이터를 이해하고 예측하는 과정이다.
따라서 데이터를 단순히 불러오는 것만으로는 충분하지 않다.
컴퓨터(특히 pandas)가 “이건 시간에 따라 변화하는 데이터야”라고 인식하도록 형태를 변환해 주는 과정, 즉 시계열 전처리(time series preprocessing) 가 꼭 필요하다.
시간 인덱스 처리
시계열 데이터를 다룰 때 가장 먼저 확인해야 하는 것은 시간 정보가 규칙적인 간격으로 정렬돼 있는가다. 날짜가 문자열로 남아 있거나, 몇 달이 빠져 있는 채로 분석을 시작하면 이후 모델링 단계에서 바로 오류를 만나게 된다. 아래 코드는 그 위험을 줄이기 위한 기본 전처리 흐름을 담고 있으며, 각 단계마다 수행 이유가 분명하다.
-
원시 데이터 구조 확인
read_csv직후head()를 통해 열 이름과 값의 범위를 눈으로 확인한다. 시계열 분석에서 열 이름을 잘못 이해하면 이후 변환에서 쉽게 실수하므로, 데이터의 구조를 확인해야 한다. -
날짜 컬럼을
datetime으로 변환Month는 문자열 상태로 들어오는데, 이를 변환하지 않으면asfreq, 이동평균, 시각화 등 Pandas의 시계열 함수를 사용할 수 없다. 변환 시에는 월-일-연도 순서를 한 번 더 검증해 문자열 파싱 오류를 예방한다. -
시간 인덱스 설정과 간격 강제
set_index("Month").asfreq("MS")를 통해 월 첫 날짜(Month Start) 기준으로 인덱스를 맞춘다.asfreq()는 데이터가 빠진 월이 있을 경우 그 자리에NaN을 채우는데, 이를 통해 결측 구간을 즉시 파악하고 보간·삭제 전략을 세울 수 있다..asfreq()는 pandas의 시계열 데이터 주기(frequency) 를 설정하거나 변경할 때 사용하는 메서드인데, "MS"는 그중 "Month Start" (월 시작) 을 의미한다. 따라서 시계열 인덱스를 매월 1일 기준으로 맞춰준다..asfreq()의 주요 인자를 정리하면 다음과 같다.옵션 의미 설명 예시 인덱스 "A"연도별 (Annual) 매년 12월 31일 기준으로 인덱스 설정 2020-12-31, 2021-12-31 "AS"연초 기준 (Annual Start) 매년 1월 1일 기준으로 인덱스 설정 2020-01-01, 2021-01-01 "Q"분기별 (Quarter End) 3월, 6월, 9월, 12월 말일 2020-03-31, 2020-06-30 "QS"분기 시작 (Quarter Start) 분기 첫 달 1일 2020-01-01, 2020-04-01 "M"월말 기준 (Month End) 매월 말일 2020-01-31, 2020-02-29 "MS"월초 기준 (Month Start) 매월 1일 2020-01-01, 2020-02-01 "W"주간 (Weekly) 매주 일요일 (기본값) 2020-01-05, 2020-01-12 "W-MON"월요일 시작 주간 매주 월요일 기준 2020-01-06, 2020-01-13 "D"일별 (Daily) 하루 단위 인덱스 2020-01-01, 2020-01-02 "B"영업일 기준 (Business Day) 주말 제외한 평일 기준 2020-01-01, 2020-01-02 "H"시간별 (Hourly) 1시간 단위 2020-01-01 00:00, 01:00, 02: "T"또는"min"분 단위 (Minute) 1분 단위 2020-01-01 00:00, 00:01 "S"초 단위 (Second) 1초 단위 2020-01-01 00:00:00, 00:00:01 -
타임존 명시 필요성 점검
이번 데이터처럼 과거 로그에 시간대가 포함돼 있지 않은 경우에는 무시해도 되지만, 서버 로그처럼 UTC 기준으로 떨어지는 데이터라면
tz_localize로 원본 타임존을 명시하고, 분석 대상 지역에 맞춰tz_convert로 변환하는 과정을 반드시 거친다.시간대 처리를 소홀히 하면 일중 패턴 분석에서 1시간씩 어긋난 결과를 얻을 수 있다.
실습 코드
# ==========================================
# 📊 AirPassengers 시계열 데이터 전처리
# ==========================================
import pandas as pd
import matplotlib.pyplot as plt
# 1️⃣ CSV 파일 불러오기
# Kaggle에서 받은 AirPassengers.csv 파일을 불러온다.
# 데이터에는 'Month'와 'Passengers' 두 개의 열이 포함되어 있다.
df = pd.read_csv("AirPassengers.csv")
# 2️⃣ 데이터 상위 5개 확인
print("원본 데이터 (상위 5행):")
print(df.head())
# 3️⃣ 'Month' 열을 날짜(datetime) 형식으로 변환
# 문자열 형식의 날짜를 datetime 형식으로 바꿔야
# 시계열 연산(예: 차분, 이동평균 등)을 수행 가능
df["Month"] = pd.to_datetime(df["Month"])
# 4️⃣ 'Month'를 인덱스로 설정하고, 월 단위(Month Start) 시계열로 지정
# asfreq("MS")는 "Month Start" 빈도로 시계열 주기 설정
df = df.set_index("Month").asfreq("MS")
# 5️⃣ 변환된 데이터 확인
print("\n시계열 인덱스 적용 후 데이터:")
print(df.head())
# 6️⃣ 데이터 기본 통계 요약
print("\n📈 데이터 통계 요약:")
print(df.describe())
# 7️⃣ 결측치 확인
print("\n결측치 확인:")
print(df.isnull().sum())
# 8️⃣ 시각화: 월별 여객 수 변화 추이
plt.figure(figsize=(10, 5))
plt.plot(df.index, df["#Passengers"], color="royalblue", linewidth=2)
plt.title("Monthly Number of Air Passengers (1949–1960)", fontsize=13)
plt.xlabel("Year")
plt.ylabel("Passengers")
plt.grid(True, linestyle="--", alpha=0.5)
plt.tight_layout()
plt.show()
# 9️⃣ 간단한 통계 해석 출력
print("\n📊 해석:")
print("• 데이터 기간:", df.index.min().strftime("%Y-%m"), " ~ ", df.index.max().strftime("%Y-%m"))
print("• 전체 관측치 수:", len(df))
print("• 월별 평균 여객 수:", round(df['#Passengers'].mean(), 2))
print("• 최대 여객 수:", df['#Passengers'].max())
print("• 최소 여객 수:", df['#Passengers'].min())
실행결과
원본 데이터 (상위 5행):
Month #Passengers
0 1949-01 112
1 1949-02 118
2 1949-03 132
3 1949-04 129
4 1949-05 121
---------------------------
시계열 인덱스 적용 후 데이터:
#Passengers
Month
1949-01-01 112
1949-02-01 118
1949-03-01 132
1949-04-01 129
1949-05-01 121
---------------------------
📈 데이터 통계 요약:
#Passengers
count 144.000000
mean 280.298611
std 119.966317
min 104.000000
25% 180.000000
50% 265.500000
75% 360.500000
max 622.000000
---------------------------
결측치 확인:
#Passengers 0
dtype: int64
---------------------------
📊 해석:
• 데이터 기간: 1949-01 ~ 1960-12
• 전체 관측치 수: 144
• 월별 평균 여객 수: 280.3
• 최대 여객 수: 622
• 최소 여객 수: 104
---------------------------
결측치와 이상치 점검
데이터 분석에서 가장 먼저 수행해야 할 일 중 하나가 결측치(Missing Value) 와 이상치(Outlier) 를 점검하는 것이다.
결측치와 이상치 점검은 단순한 데이터 정제(cleaning) 단계를 넘어, 분석의 신뢰성과 모델의 예측력을 결정짓는 핵심 과정으로 볼 수 있다.
먼저, 결측치는 데이터가 일부 누락되거나 기록되지 않은 상태를 의미한다.
센서의 일시적 오류, 수집 과정의 누락, 혹은 시스템 문제로 인해 특정 시점의 값이 비어 있을 수 있다.
이러한 결측치를 그대로 두면 통계 분석에서 평균, 분산, 상관계수 등 기본 지표가 왜곡되며,
머신러닝 모델은 결측 데이터를 처리하지 못하고 오류를 발생시키거나 부정확한 예측을 하게 된다.
따라서 결측치는 보간(interpolation), 이전값 대체(ffill), 도메인 지식 기반 보정 등을 통해 적절히 채워야 한다.
반면, 이상치는 정상적인 데이터 패턴에서 벗어난 비정상적인 값이다.
예를 들어 센서의 순간적인 오작동이나 외부 환경 요인으로 인해 극단적으로 높은 값이나 낮은 값이 기록될 수 있다.
이상치를 그대로 분석에 포함하면 평균값이 급격히 변하거나 회귀모델의 기울기가 왜곡되는 등,
모델이 데이터의 ‘일반적 패턴’을 올바르게 학습하지 못하게 된다.
따라서 이상치는 사분위수 범위(IQR), 이동평균 기반 편차, 도메인 기준 임계값 등을 이용해 탐지하고,
필요에 따라 보정 또는 제거해야 한다.
결국 결측치와 이상치 점검은 단순한 데이터 정리가 아니라, 데이터의 신뢰성(reliability), 정확성(accuracy), 그리고 모델의 일반화 능력(generalization) 을 확보하기 위한 필수 과정이다.
이 단계를 소홀히 하면, 이후의 모든 분석이나 예측 결과가 왜곡될 위험이 있으며, 잘못된 의사결정으로 이어질 수 있다.
따라서 분석자는 모델링 이전에 반드시 결측치와 이상치를 면밀히 점검하고, 그 원인과 영향을 이해한 후 적절한 처리를 수행해야 한다.
데이터셋: Air Quality Time Series Data (UCI/Kaggle)
- 직접 다운로드 : click me
Air Quality 데이터셋 변수
| 번호 | 변수명 | 설명 | 단위 | 비고 |
|---|---|---|---|---|
| 0 | Date | 측정 날짜 | DD/MM/YYYY | 예: 10/03/2004 |
| 1 | Time | 측정 시각 | HH.MM.SS | 예: 18.00.00 |
| 2 | CO(GT) | 참조 분석기(reference analyzer)를 이용한 일산화탄소(CO) 시간 평균 농도 | mg/m³ | 대기 오염의 주요 지표 |
| 3 | PT08.S1(CO) | 주석 산화물(SnO₂) 센서의 응답값 (CO 감지용) | 센서 단위 | CO 농도와 관련 |
| 4 | NMHC(GT) | 참조 분석기로 측정한 비메탄 탄화수소(NMHC) 농도 | µg/m³ | 산업 및 차량 배출가스 관련 |
| 5 | C6H6(GT) | 참조 분석기로 측정한 벤젠(Benzene) 농도 | µg/m³ | 발암물질, 대기질 지표 |
| 6 | PT08.S2(NMHC) | 이산화티타늄(TiO₂) 센서의 응답값 (NMHC 감지용) | 센서 단위 | NMHC 농도와 관련 |
| 7 | NOx(GT) | 참조 분석기로 측정한 질소산화물(NOx) 농도 | ppb | 차량 배출, 대기오염 주요 요인 |
| 8 | PT08.S3(NOx) | 텅스텐 산화물(WO₃) 센서의 응답값 (NOx 감지용) | 센서 단위 | NOx 감지 |
| 9 | NO2(GT) | 참조 분석기로 측정한 이산화질소(NO₂) 농도 | µg/m³ | 인체 유해 가스 |
| 10 | PT08.S4(NO2) | 텅스텐 산화물(WO₃) 센서의 응답값 (NO₂ 감지용) | 센서 단위 | NO₂ 감지 |
| 11 | PT08.S5(O3) | 인듐 산화물(In₂O₃) 센서의 응답값 (오존 O₃ 감지용) | 센서 단위 | 오존 농도 감지 |
| 12 | Temperature | 온도 | °C | 실내 공기 온도 |
| 13 | Relative Humidity | 상대 습도 | % | 습도 센서 측정값 |
| 14 | AH (Absolute Humidity) | 절대 습도 | g/m³ | 공기 중 수증기량 |
특징: 시간별 또는 일별로 측정된 대기 오염 물질(PM2.5, PM10, NOx 등) 데이터이며, 일부 시점에 결측치 또는 비정상값(-200 등)이 포함되어 있음.
실습 목표
1) 시계열 인덱스 처리 및 기본사항 확인
2) 결측치 탐지 및 보정 (보간, ffill/bfill 등)
3) 이상치 탐지 및 보정
4) 대기질 추세 분석
시계열 인덱스 처리 및 기본사항 확인
모듈 임포트 에러가 나는 경우
ImportError: Missing optional dependency 'openpyxl'. Use pip or conda to install openpyxl.
pip install openpyxl
실습 코드
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 1) 엑셀 파일 로드 (openpyxl 패키지가 필요함)
# - AirQualityUCI.xlsx 파일을 불러옴
# - sheet_name=0 : 첫 번째 시트를 읽음
# - engine="openpyxl" : .xlsx 파일을 처리하는 데 필요한 엔진 지정
df = pd.read_excel(
"AirQualityUCI.xlsx",
sheet_name=0,
engine="openpyxl"
)
# 2) Date/Time 정규화
# - Date: 어떤 타입이든 datetime으로 변환하여 날짜 형식을 통일
# - dayfirst=True : 날짜가 'DD/MM/YYYY' 형식일 때 올바르게 인식되도록 지정
# - errors="coerce" : 변환 불가능한 값은 NaT(Not a Time)으로 처리하여 오류 방지
date_ser = pd.to_datetime(df["Date"], dayfirst=True, errors="coerce")
# datetime 타입의 날짜를 문자열 'YYYY-MM-DD' 형식으로 변환
# 문자열로 만들어 두면 나중에 Time과 안전하게 결합할 수 있음
date_str = date_ser.dt.strftime("%Y-%m-%d")
# Time 컬럼 정규화
# - Time 값이 HH.MM.SS 형식으로 되어 있으므로, 점(.)을 콜론(:)으로 바꿈
# - astype(str) : 숫자나 결측값 등 모든 값을 문자열로 통일
# - str.replace(".", ":", n=2, regex=False) : 앞에서 두 번만 '.'을 ':'로 교체 (HH.MM.SS → HH:MM:SS)
# - str.strip() : 앞뒤 공백을 제거
time_str = (
df["Time"]
.astype(str)
.str.replace(".", ":", n=2, regex=False)
.str.strip()
)
# Time 문자열 중 길이가 0인 항목(즉, 비어 있는 값)을 찾아서
# "00:00:00"으로 채워주는 코드임.
# -> Time 정보가 비어 있으면 자정(00시)으로 대체하여 Datetime 생성 시 오류를 방지
time_str = time_str.where(time_str.str.len() > 0, "00:00:00")
# 3) 최종 Datetime 생성 (문자열 결합 후 파싱)
df["Datetime"] = pd.to_datetime(date_str + " " + time_str, errors="coerce")
# 4) 인덱스/주기 설정
df = df.set_index("Datetime").sort_index().asfreq("H") # 시간 단위(Hourly)
# 5) 센서 오류값 -200을 결측치로 처리 (UCI Air Quality 관례)
num_cols = df.select_dtypes(include="number").columns
df[num_cols] = df[num_cols].replace(-200, np.nan)
# 6) 확인
print(df.tail())
print("\n결측치 개수:")
print(df.isnull().sum())
# 7) 간단 시각화: CO(GT) 농도 시계열 그래프
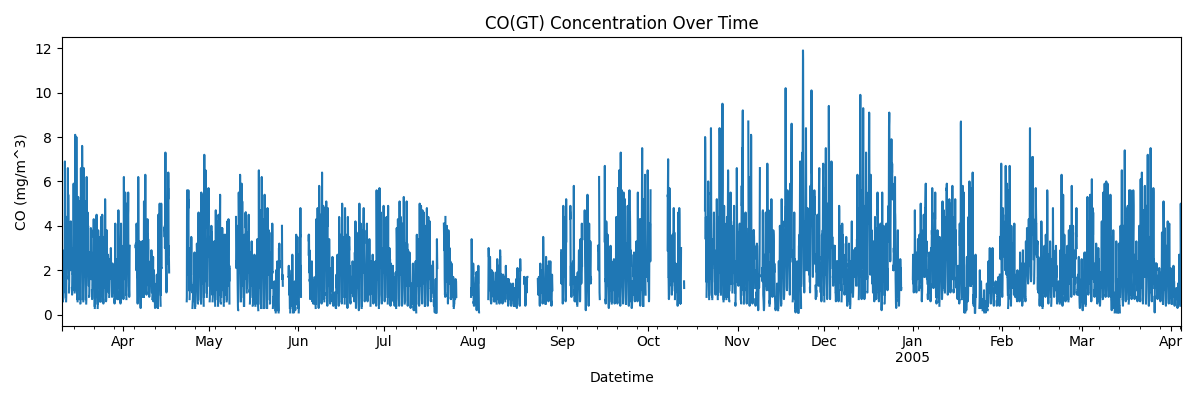
if "CO(GT)" in df.columns:
ax = df["CO(GT)"].plot(figsize=(12, 4), title="CO(GT) Concentration Over Time")
ax.set_xlabel("Datetime")
ax.set_ylabel("CO (mg/m^3)")
plt.tight_layout()
plt.show()
else:
print("Column 'CO(GT)' not found in the DataFrame.")
실행 결과
[5 rows x 15 columns]
결측치 개수:
Date 0
Time 0
CO(GT) 1683
PT08.S1(CO) 366
NMHC(GT) 8443
C6H6(GT) 366
PT08.S2(NMHC) 366
NOx(GT) 1639
PT08.S3(NOx) 366
NO2(GT) 1642
PT08.S4(NO2) 366
PT08.S5(O3) 366
T 366
RH 366
AH 366
dtype: int64
결측치 탐지 및 보정
시계열 데이터에서는 센서 오류, 통신 지연, 측정 중단 등으로 인해 결측치(missing value) 가 자주 발생한다.
결측치는 분석이나 모델 학습에 직접적인 영향을 주므로, 반드시 탐지하고 적절히 보정해야 한다.
AirQualityUCI.xlsx에 포함된 결측치
Date 0
Time 0
CO(GT) 1683
PT08.S1(CO) 366
NMHC(GT) 8443
C6H6(GT) 366
PT08.S2(NMHC) 366
NOx(GT) 1639
PT08.S3(NOx) 366
NO2(GT) 1642
PT08.S4(NO2) 366
PT08.S5(O3) 366
T 366
RH 366
AH 366
결측치를 처리하는 대표적인 방법은 다음과 같다.
| 방법 | 설명 | 특징 |
|---|---|---|
interpolate() |
이전·다음 값의 선형 관계를 기반으로 보간 (보간법) |
연속적인 시계열에 적합 |
ffill()(forward fill) |
직전의 관측값으로 결측치 채움 | 센서 일시 오류에 유용 |
bfill()(backward fill) |
이후의 관측값으로 결측치 채움 | 데이터 앞부분의 공백에 사용 |
선형보간법(Linear Interpolation)
데이터 사이에 빠진 값을 이전 값과 다음 값을 직선(선형)으로 연결해서 그 중간 값을 채워 넣는 방법이다.
즉, “결측된 구간에서도 값이 일정한 속도로 변한다고 가정하고, 그 사이의 값을 계산”하는 접근법이다.
| 시간 | 온도(℃) |
|---|---|
| 10시 | 20 |
| 11시 | NaN (측정 누락) |
| 12시 | 24 |

이때 11시의 온도는 실제로 측정되지 않았다.
그런데 10시엔 20℃, 12시엔 24℃니까 "11시는 두 값의 중간쯤인 22℃ 정도일 거야"라고 선형적으로 추정 한다.
두 점 \((x_1, y_1)\), \((x_2, y_2)\) 사이의 선형 보간식은 다음과 같다.
또는,
즉, \(x\)가 \(x_1\)과 \(x_2\) 사이에 있을 때, 두 점을 잇는 직선의 방정식을 이용해 \(y(x)\) 값을 추정하는 방법이다.
구현 예시
# 결측치 보간 예시
df_interp = df.copy()
# (1) 선형 보간법으로 연속 구간 채우기
df_interp = df_interp.interpolate(method="linear", limit_direction="both")
# (2) 여전히 남은 결측치는 ffill, bfill로 보완
df_interp = df_interp.fillna(method="ffill").fillna(method="bfill")
# 보정 후 결측치 재확인
print("보정 후 결측치 합계:", df_interp.isnull().sum().sum())
보정 후 결측치 합계: 0
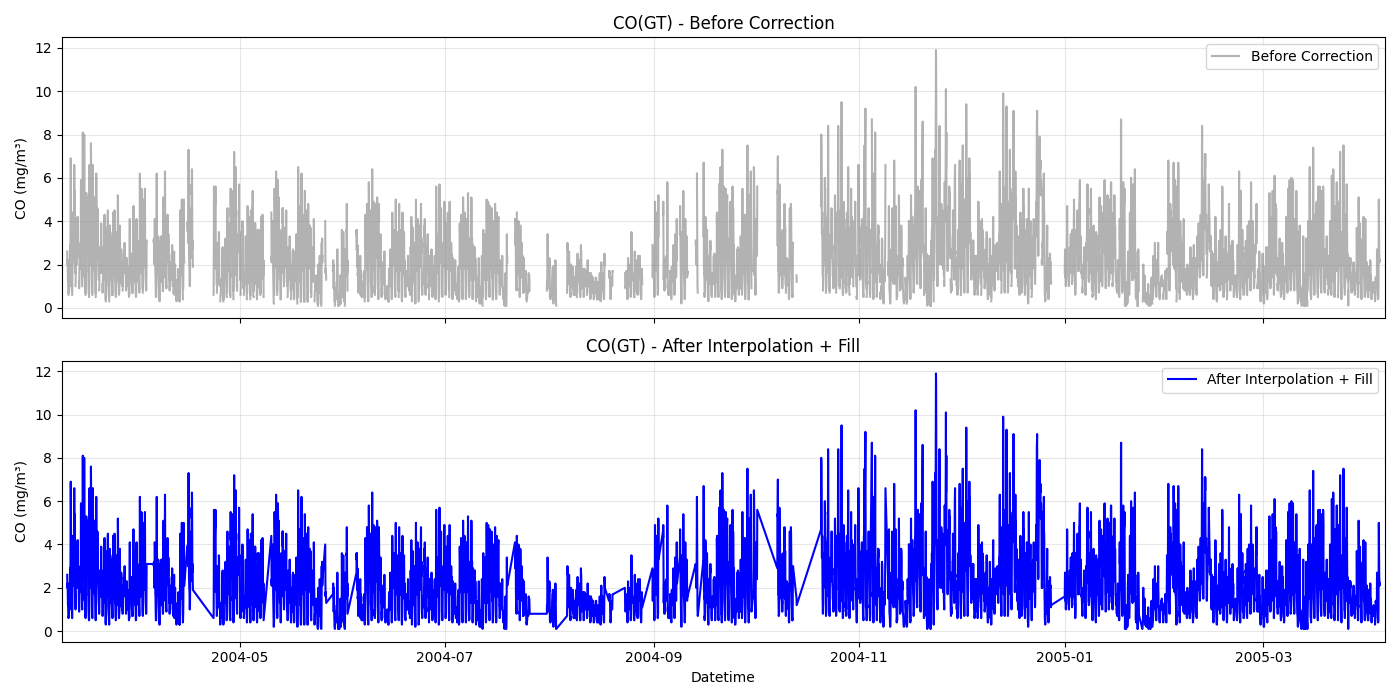
보정 전후 시각화 예시
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 1️⃣ 엑셀 파일 로드
df = pd.read_excel("AirQualityUCI.xlsx", sheet_name=0, engine="openpyxl")
# 2️⃣ 시간 정보 정규화
df["Time"] = (
df["Time"].astype(str)
.str.replace(".", ":", n=2, regex=False)
.str.strip()
.where(lambda s: s.str.len() > 0, "00:00:00")
)
date_ser = pd.to_datetime(df["Date"], dayfirst=True, errors="coerce")
date_str = date_ser.dt.strftime("%Y-%m-%d")
df["Datetime"] = pd.to_datetime(date_str + " " + df["Time"], errors="coerce")
# 3️⃣ Datetime 인덱스 설정 및 시간 주기 지정
df = df.set_index("Datetime").sort_index().asfreq("h")
# 4️⃣ 센서 오류값(-200)을 NaN으로 변환
num_cols = df.select_dtypes(include=np.number).columns
df[num_cols] = df[num_cols].replace(-200, np.nan)
df[num_cols] = df[num_cols].infer_objects(copy=False)
# 5️⃣ 결측치 보간 (선형보간 + ffill + bfill)
df_interp = df[num_cols].interpolate(
method="linear",
limit_direction="both" # "forward" + "backward" 둘 다 고려해서 양쪽 값의 평균 경로로 보간하는 방식
).ffill().bfill()
# 6️⃣ 시각화 대상 변수 선택
target_col = "CO(GT)"
before = df[target_col]
after = df_interp[target_col]
# 7️⃣ 결측이 있었던 구간 찾기 (시각적 강조용)
mask_nan = before.isna()
if mask_nan.sum() > 0:
first_nan = mask_nan[mask_nan].index.min()
last_nan = mask_nan[mask_nan].index.max()
start_zoom = first_nan - pd.Timedelta(days=2)
end_zoom = last_nan + pd.Timedelta(days=2)
else:
start_zoom = df.index.min()
end_zoom = start_zoom + pd.Timedelta(days=7)
# 8️⃣ 상하 2단 subplot 시각화
fig, axes = plt.subplots(2, 1, figsize=(14, 7), sharex=True)
# --- 상단: 보정 전 ---
axes[0].plot(before.index, before, color="gray", alpha=0.6, label="Before Correction")
axes[0].set_title(f"{target_col} - Before Correction")
axes[0].set_ylabel("CO (mg/m³)")
axes[0].grid(alpha=0.3)
axes[0].legend()
# --- 하단: 보정 후 ---
axes[1].plot(after.index, after, color="blue", linewidth=1.5, label="After Interpolation + Fill")
axes[1].set_title(f"{target_col} - After Interpolation + Fill")
axes[1].set_xlabel("Datetime")
axes[1].set_ylabel("CO (mg/m³)")
axes[1].grid(alpha=0.3)
axes[1].legend()
# 확대 영역 설정
axes[0].set_xlim(start_zoom, end_zoom)
axes[1].set_xlim(start_zoom, end_zoom)
plt.tight_layout()
plt.show()
실행 결과
Date Time CO(GT) PT08.S1(CO) ... PT08.S5(O3) T RH
AH
Datetime ...
2005-04-04 10:00:00 2005-04-04 10:00:00 3.1 1314.25 ... 1728.50 21.850 29.250 0.756824
1864
2005-04-04 12:00:00 2005-04-04 12:00:00 2.4 1142.00 ... 1092.00 26.900 18.350 0.640649
2005-04-04 13:00:00 2005-04-04 13:00:00 2.1 1002.50 ... 769.75 28.325 13.550 0.513866
2005-04-04 14:00:00 2005-04-04 14:00:00 2.2 1070.75 ... 816.00 28.500 13.125 0.502804
[5 rows x 15 columns]
보정 후 전체 결측치 수: 0
이상치 탐지 및 보정
시계열 데이터에는 센서 오류, 통신 문제, 일시적 급변 현상 등으로 인해 정상 범위를 벗어난 이상치(outlier) 가 포함될 수 있다.
이상치는 모델의 학습과 예측 정확도를 떨어뜨리므로, 탐지 → 판단 → 보정(또는 제거) 의 절차가 필요하다.
이상치 탐지 방법
-
IQR(사분위 범위) 기반 탐지 \[ IQR = Q3 - Q1 \] \[ \text{하한} = Q1 - 1.5 \times IQR, \quad \text{상한} = Q3 + 1.5 \times IQR \]
상한보다 크거나 하한보다 작은 값은 이상치로 간주한다.
-
이동 평균(rolling mean) 기반 탐지 \[ |x_t - \bar{x}_t| > k \times \sigma_t \]
- \(\bar{x}_t\): 최근 일정 구간의 평균
- \(\sigma_t\): 최근 구간의 표준편차
- \(k\): 임계값(보통 2~3)
이상치 탐지 실습
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 1. 데이터 로드 및 준비
df = pd.read_excel("AirQualityUCI.xlsx", sheet_name=0, engine="openpyxl")
df["Time"] = df["Time"].astype(str).str.replace(".", ":", n=2, regex=False).str.strip()
date_ser = pd.to_datetime(df["Date"], dayfirst=True, errors="coerce")
date_str = date_ser.dt.strftime("%Y-%m-%d")
df["Datetime"] = pd.to_datetime(date_str + " " + df["Time"], errors="coerce")
df = df.set_index("Datetime").sort_index().asfreq("h")
# 2. 숫자형 컬럼만 추출 및 센서 오류값(-200) 제거
num_cols = df.select_dtypes(include=np.number).columns
df[num_cols] = df[num_cols].replace(-200, np.nan)
# 3. 대상 컬럼 선택
target_col = "CO(GT)"
series = df[target_col].dropna()
# 4. IQR 계산
Q1 = series.quantile(0.25)
Q3 = series.quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
# 5. 이상치 탐지
outliers = series[(series < lower_bound) | (series > upper_bound)]
print(f"이상치 개수: {len(outliers)}")
print(f"상한: {upper_bound:.2f}, 하한: {lower_bound:.2f}")
# 6. 시각화
plt.figure(figsize=(12,5))
plt.plot(series.index, series, label="Original", color="gray")
plt.scatter(outliers.index, outliers, color="red", label="Outliers")
plt.title("Outlier Detection using IQR Method")
plt.xlabel("Datetime")
plt.ylabel("CO (mg/m³)")
plt.legend()
plt.tight_layout()
plt.show()
실행 결과
이상치 개수: 215
상한: 5.60, 하한: -1.60
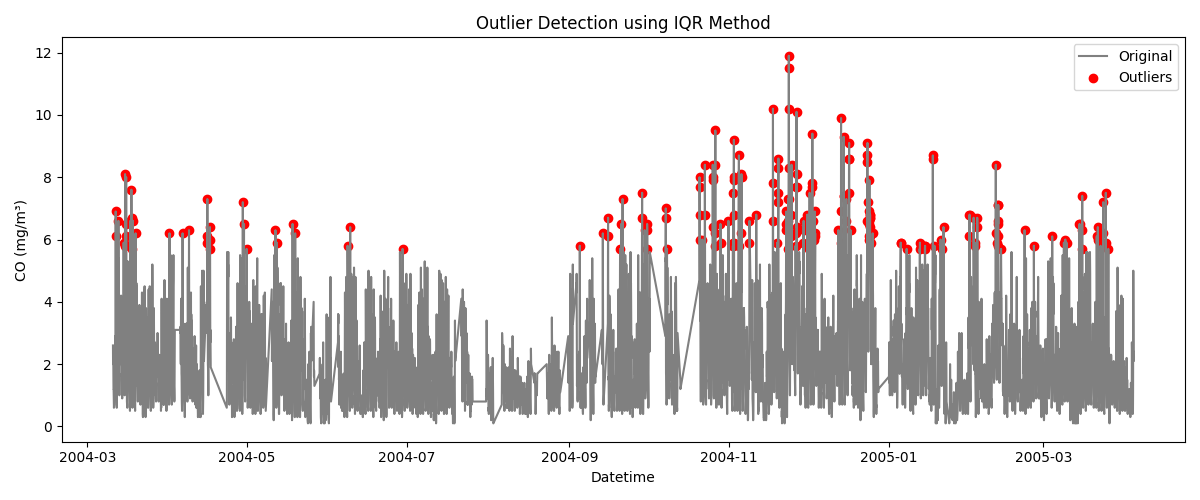
이상치 보정 방법
| 방법 | 설명 | 예시 |
|---|---|---|
| 삭제(drop) | 명백한 오류값 제거 | 데이터 손실 가능 |
| 평균/중앙값 대체 | 주변 통계값으로 치환 | 극단값 완화 |
| 보간(interpolation) | 시간 흐름 고려 선형 대체 | 연속성 유지 |
| 윈도우 스무딩 | 급격한 변화 완화 | 장기 추세 반영에 유리 |
이동평균과 스무딩
이동평균(Moving Average)의 개념
-
일정한 창(window)에 포함된 관측값의 평균으로, 단기 변동을 완화하고 장기 추세를 강조한다.
-
창 크기가 클수록 노이즈는 줄어들지만 반응 속도가 느려지므로, 분석 목적에 맞게 적정 값을 선택해야 한다.
-
가중 이동평균(Weighted Moving Average)이나 지수평활(Exponential Smoothing)처럼 최근 관측치에 더 큰 가중치를 주는 변형도 실무에서 자주 사용된다.
-
윈도우 스무딩(Window Smoothing)이란?
윈도우 스무딩은 시계열 데이터의 단기적인 요동(잡음) 을 완화하고, 전체적인 장기 추세(trend) 를 부드럽게 보기 위해 사용하는 기법
윈도우(window)란 특정 시점을 중심으로 한 일정 개수의 관측치 구간을 의미한다. 예를 들어 “이동 평균(rolling mean)”을 구할 때 최근 5시간 데이터를 하나의 윈도우로 삼아 평균을 낸다면, 현재 값은 이전 5시간 동안의 평균값으로 대체하는 방식이다.
윈도우 크기를 \( n \)이라 할 때, 시점 \( t \)에서의 이동 평균(또는 스무딩된 값)은 다음과 같이 정의된다.
중앙값 대체
여기서,
-
\( \tilde{y_t} \): 스무딩된(평활화된) 값
-
\( n \): 윈도우 크기 (예: 3시간, 7일 등)
-
\( y_i \): 시점 \( i \)의 실제 관측값
-
\( \sum_{i=t-n+1}^{t} \): 최근 \( n \)개의 시점 데이터의 합
중앙값 대체 실습 코드
# 앞 예제의 마지막에 이어서 코딩
median = series.median()
series_corrected = series.copy()
series_corrected[outliers.index] = median
plt.figure(figsize=(12,5))
plt.plot(series.index, series, label="Before Correction", color="gray", alpha=0.6)
plt.plot(series_corrected.index, series_corrected, label="After Correction", color="blue", linewidth=1.2)
plt.scatter(outliers.index, outliers, color="red", label="Detected Outliers")
plt.title("Outlier Correction (Median Replacement)")
plt.xlabel("Datetime")
plt.ylabel("CO (mg/m³)")
plt.legend()
plt.tight_layout()
plt.show()
실행 결과
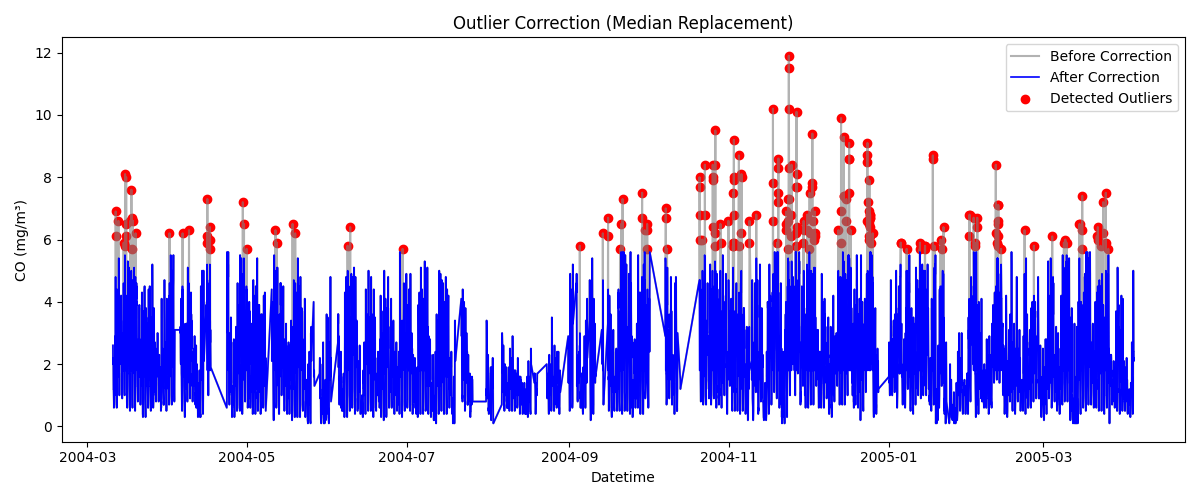
종합 실습 - 대기질 추세 분석
| 분석 관점 | 설명 |
|---|---|
| 장기 추세(Long-term Trend) | 1년 단위로 CO, NOx, Benzene 등의 평균 농도 변화를 분석 (예: 겨울철 오염 증가) |
| 계절별 변화(Seasonality) | 월별 또는 분기별 평균값 비교를 통해 봄·여름·가을·겨울 간 대기질 차이 탐색 |
| 일중 패턴(Daily Pattern) | 하루 중 오전/오후/야간의 오염물질 변화 관찰 (예: 출퇴근 시간대 CO 증가) |
| 센서 간 상관관계 | 여러 센서(PT08.S1~S5)와 오염물질 간의 관계 파악 |
# ============================================
# Air Quality UCI 시계열 종합 실습 코드
# - 파일: AirQualityUCI.xlsx
# - 전처리: Date/Time → Datetime, asfreq('h'), -200→NaN, 보간+ffill/bfill
# - 분석: 장기추세, 계절별 변화, 일중패턴, 센서 상관(히트맵)
# ============================================
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# -------------------------------
# 1) 데이터 로드 + Datetime 정규화
# -------------------------------
# (필요 패키지) pip install openpyxl seaborn
df = pd.read_excel("AirQualityUCI.xlsx", sheet_name=0, engine="openpyxl")
# Time이 HH.MM.SS 형태인 경우가 있어 '.' → ':'로 교체, 공백/NaN은 00:00:00으로 대체
df["Time"] = (
df["Time"].astype(str)
.str.replace(".", ":", n=2, regex=False)
.str.strip()
.where(lambda s: s.str.len() > 0, "00:00:00")
)
# Date를 datetime으로 파싱 후 문자열화(YYYY-MM-DD) → Time과 안전하게 결합
date_ser = pd.to_datetime(df["Date"], dayfirst=True, errors="coerce")
date_str = date_ser.dt.strftime("%Y-%m-%d")
df["Datetime"] = pd.to_datetime(date_str + " " + df["Time"], errors="coerce")
# Datetime 인덱스 설정 + 시간 주기 명시 (h)
df = df.set_index("Datetime").sort_index().asfreq("h")
# -------------------------------
# 2) 센서 오류값 -200 → NaN, 숫자형 컬럼만 보간
# -------------------------------
num_cols = df.select_dtypes(include=np.number).columns
df[num_cols] = df[num_cols].replace(-200, np.nan)
# 선형보간(양방향) → 남은 NaN은 ffill/bfill로 보완
df[num_cols] = df[num_cols].infer_objects(copy=False)
df[num_cols] = df[num_cols].interpolate(method="linear", limit_direction="both")
df[num_cols] = df[num_cols].ffill().bfill()
# 분석에 자주 쓰는 주요 컬럼 후보 (실제 파일에 맞춰 자동 선택)
candidates = ["CO(GT)", "NOx(GT)", "NO2(GT)", "C6H6(GT)"]
used = [c for c in candidates if c in df.columns]
if not used:
raise KeyError("분석용 주요 컬럼(CO(GT), NOx(GT), NO2(GT), C6H6(GT))을 찾을 수 없습니다. 파일 컬럼명을 확인하세요.")
print("[사용 컬럼]", used)
# --------------------------------
# 3) 장기 추세: 30일 이동평균(rolling)
# --------------------------------
# 시간 단위가 시간(h)이므로 30일 ≈ 30*24=720시간 윈도우
roll = df[used].rolling(window=24*30, min_periods=1).mean()
plt.figure(figsize=(12, 5))
for col in used:
plt.plot(roll.index, roll[col], label=f"{col} (30D MA)")
plt.title("Long-term Trend (30-day Moving Average)")
plt.xlabel("Datetime")
plt.ylabel("Concentration (unit varies)")
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# --------------------------------
# 4) 계절별 변화: 월별 평균 (Monthly mean)
# --------------------------------
monthly_mean = df[used].resample("M").mean()
plt.figure(figsize=(12, 5))
for col in used:
plt.plot(monthly_mean.index, monthly_mean[col], marker="o", label=col)
plt.title("Seasonality: Monthly Mean")
plt.xlabel("Month")
plt.ylabel("Concentration (unit varies)")
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# --------------------------------
# 5) 일중 패턴: 시간대별 평균 (Hour-of-day)
# --------------------------------
# 하루 0~23시 기준 평균
hourly_pattern = df[used].groupby(df.index.hour).mean()
plt.figure(figsize=(12, 5))
for col in used:
plt.plot(hourly_pattern.index, hourly_pattern[col], marker="o", label=col)
plt.xticks(range(0, 24))
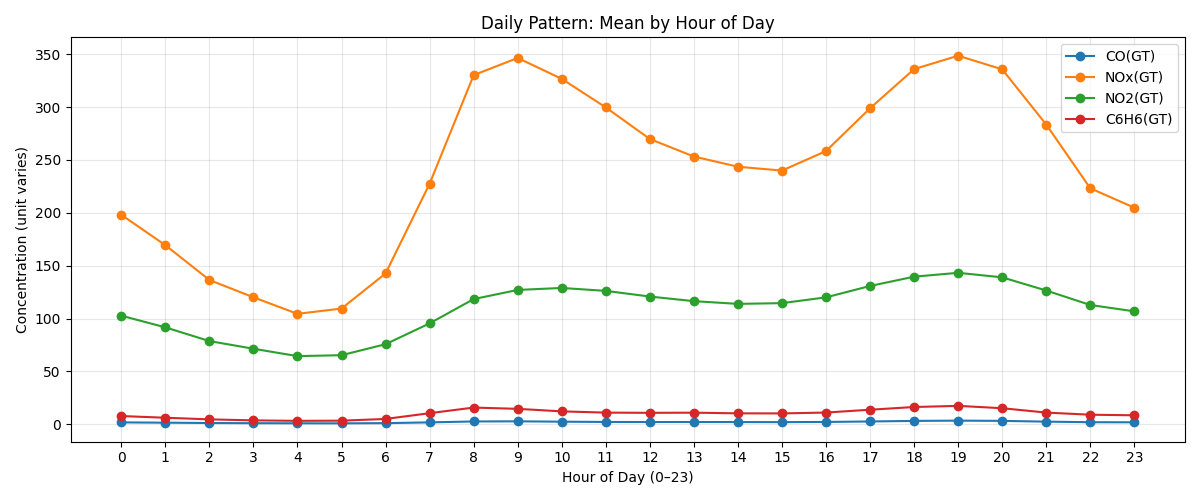
plt.title("Daily Pattern: Mean by Hour of Day")
plt.xlabel("Hour of Day (0–23)")
plt.ylabel("Concentration (unit varies)")
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
# --------------------------------
# 6) 센서 간 상관관계: 히트맵
# --------------------------------
# 수치형 전체 상관 또는 주요컬럼만
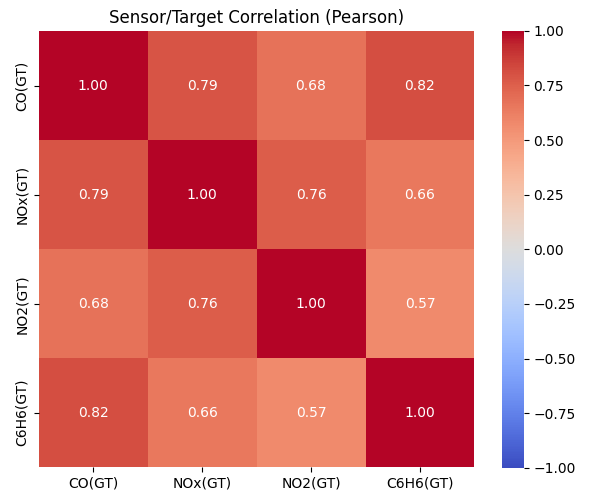
corr = df[used].corr(method="pearson")
plt.figure(figsize=(6, 5))
sns.heatmap(corr, annot=True, fmt=".2f", cmap="coolwarm", vmin=-1, vmax=1, square=True, cbar=True)
plt.title("Sensor/Target Correlation (Pearson)")
plt.tight_layout()
plt.show()
# --------------------------------
# 7) 보너스: 결과 요약 출력
# --------------------------------
print("\n[월별 평균 상위 5행]")
print(monthly_mean.head())
print("\n[시간대별 평균 상위 5행]")
print(hourly_pattern.head())
print("\n[상관행렬]")
print(corr)
실행 결과
[사용 컬럼] ['CO(GT)', 'NOx(GT)', 'NO2(GT)', 'C6H6(GT)']
[월별 평균 상위 5행]
CO(GT) NOx(GT) NO2(GT) C6H6(GT)
Datetime
2004-03-31 2.249804 140.054902 101.051961 9.935104
2004-04-30 2.138194 133.404861 91.852083 10.297856
2004-05-31 1.921841 122.704301 92.790323 10.639145
2004-06-30 1.864514 117.509028 91.445139 10.348168
2004-07-31 1.709812 123.196909 102.146505 10.595534
[시간대별 평균 상위 5행]
CO(GT) NOx(GT) NO2(GT) C6H6(GT)
Datetime
0 1.846334 198.088869 102.727612 7.852139
1 1.567172 169.398402 91.692612 6.236522
2 1.262307 136.461424 78.734202 4.704003
3 1.079787 120.127575 71.472095 3.749056
4 0.991097 104.478598 64.486141 3.312346
[상관행렬]
CO(GT) NOx(GT) NO2(GT) C6H6(GT)
CO(GT) 1.000000 0.791297 0.675975 0.816538
NOx(GT) 0.791297 1.000000 0.763096 0.655011
NO2(GT) 0.675975 0.763096 1.000000 0.570459
C6H6(GT) 0.816538 0.655011 0.570459 1.000000
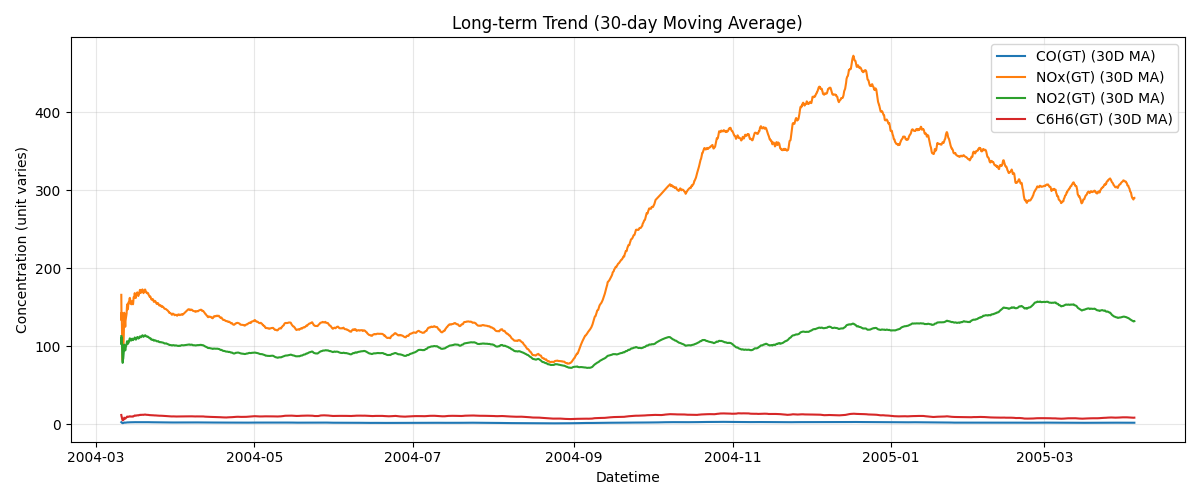
계절별 변화(Seasonality)
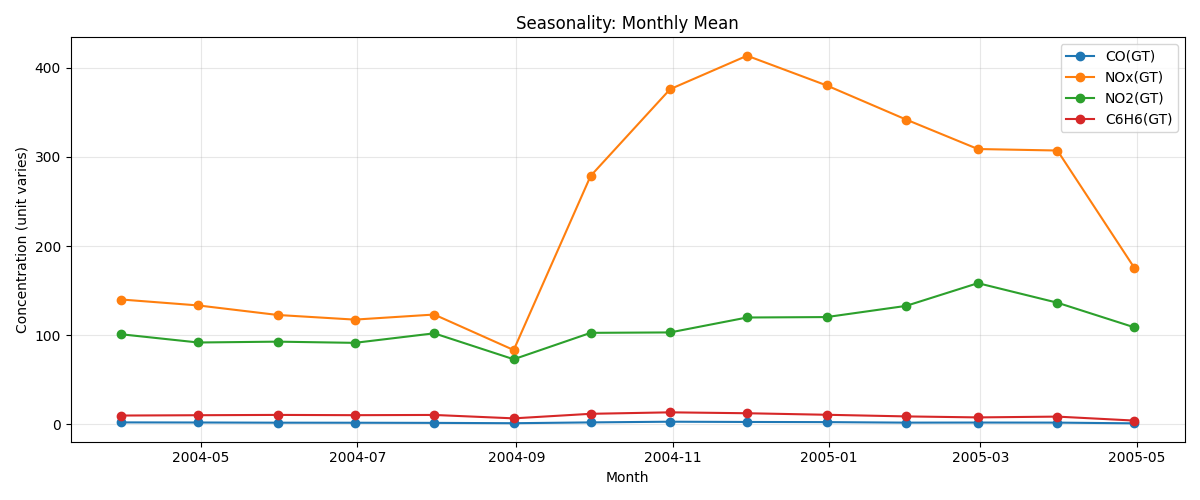
일중 패턴(Daily Pattern)
센서 간 상관관계
시계열 분해 (Time Series Decomposition)
시계열(time series) 데이터는 단순히 시간에 따른 값의 나열이 아니라, 다양한 패턴의 합성으로 이루어진다.
이러한 패턴을 분리해내는 과정을 시계열 분해(Time Series Decomposition) 라고 한다.
시계열 분해를 하는 이유
| 목적 | 설명 | 예시 |
|---|---|---|
| 구조 이해 | 추세·계절·노이즈를 분리하여 패턴 파악 | 온도 상승 + 계절 변동 |
| 예측 개선 | 비정상성 제거로 모델 성능 향상 | ARIMA 학습 안정화 |
| 이상 탐지 | 잔차를 통해 예외적 사건 탐색 | 폭염으로 인한 전력 급등 |
| 해석력 향상 | 각 요인의 기여도를 설명 | 매출 상승 원인 분리 |
시계열의 구성 요소 (Components of a Time Series)
시계열 데이터는 일반적으로 다음 네 가지 성분의 합으로 표현할 수 있다.
| 구성 요소 | 설명 | 예시 |
|---|---|---|
| 추세 (Trend, \(T_t\)) |
데이터가 장기간에 걸쳐 증가하거나 감소하는 전반적 경향 |
평균기온 상승, 판매량 증가 |
| 계절성 (Seasonality, \(S_t\)) |
일정 주기마다 반복되는 주기적 패턴 |
월별 전기 사용량, 요일별 교통량 |
| 순환성 (Cyclic, \(C_t\)) |
경기 변동과 같은 비정기적 장기 요동 |
경기 침체, 호황 주기 |
| 불규칙성 (Irregular, \(I_t\)) |
예측 불가능한 우연적 요인 |
천재지변, 이벤트 효과 |
대부분의 분석에서는 \(C_t\)와 \(I_t\)를 합쳐서 단순히 잔차(residual) 로 다루기도 한다.
분해 방식 (Types of Decomposition)
시계열 성분이 어떻게 결합되어 있는가에 따라 두 가지 방식으로 분해할 수 있다.
가법모형 (Additive Model)
-
각 성분이 단순히 더해진 형태
-
성분의 진폭이 일정한 경우 (예: 월별 온도 변화)
승법모형 (Multiplicative Model)
-
각 성분이 곱으로 결합된 형태
-
데이터의 변동 폭이 시간에 따라 달라질 때 (예: 매출액이 점점 커지며 변동 폭도 커질 때)
판별 팁:
그래프에서 계절 변동 폭이 일정하면 가법모형, 변동 폭이 추세와 함께 커지면 승법모형을 사용한다.
시계열 분해 실습
# 통계 패키지 설치
pip install statsmodels
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
# 예시 데이터 (월별 대기오염 농도)
date_rng = pd.date_range(start='2020-01', end='2023-01', freq='ME')
data = {
'PM10': [80,75,70,65,90,100,95,85,80,75,70,65,
90,100,95,85,80,75,70,65,90,100,95,85,
80,75,70,65,90,100,95,85,80,75,70,65]
}
df = pd.DataFrame(data, index=date_rng)
# -------------------------------
# 1️⃣ 가법모형 (Additive Model)
# -------------------------------
result_add = seasonal_decompose(df['PM10'], model='additive')
fig1 = result_add.plot()
plt.show()
# -------------------------------
# 2️⃣ 승법모형 (Multiplicative Model)
# -------------------------------
result_mul = seasonal_decompose(df['PM10'], model='multiplicative')
fig2 = result_mul.plot()
plt.show()
실행 결과
- 시계열 분해 - 가법 (Additive) 모형 적용 결과
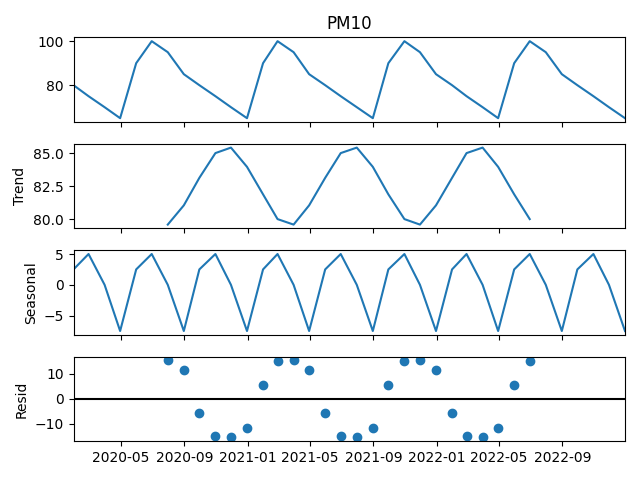
- 시계열 분해 - 승법 (Multiplicative) 모형 적용 결과
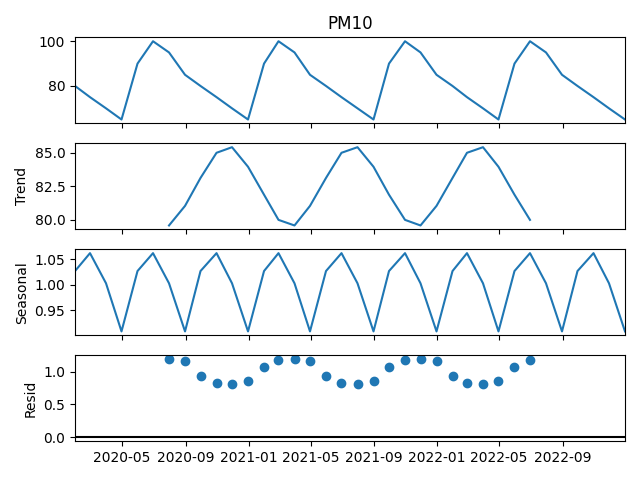
정상성(Stationarity)과 차분(Differencing)
정상성의 개념과 필요성
ARIMA, SARIMA, ARMA 등 전통적 시계열 모델은 데이터가 정상적(stationary) 일 때만 통계적으로 타당한 예측이 가능하다.
즉, 정상성(stationarity)이란 시간이 지나도 데이터의 통계적 성질(평균, 분산, 공분산 등)이 변하지 않는 성질을 말한다.
| 항목 | 내용 |
|---|---|
| 정의 | 시간에 따라 평균, 분산, 공분산이 일정한 시계열 |
| 의의 | 모델이 안정적으로 동작하고 미래 예측의 타당성을 확보 |
| 비정상 예시 | 꾸준히 증가하는 매출, 계절적 반복이 있는 데이터 |
| 정상 예시 | 평균을 중심으로 진동하는 노이즈형 데이터 |
단위근 검정 (Augmented Dickey-Fuller Test)
단위근(Unit Root) 은 시계열이 자기 자신의 과거값에 강하게 의존하여 시간이 지나도 충격이 사라지지 않고 누적되는 성질을 의미한다.
즉, 단위근이 존재하면 시계열이 비정상(Non-stationary) 하다는 뜻이다.
수식적 표현
가장 단순한 자기회귀(AR(1)) 모델을 생각해보자.
- \( y_t \): 현재 시점의 값
- \( y_{t-1} \): 이전 시점의 값
- \( \epsilon_t \): 백색잡음 (white noise)
- \( \phi \): 자기회귀 계수
단위근이 존재하는 경우
만약 \( \phi = 1 \) 이라면,
시간이 지날수록 평균과 분산이 변하는 비정상 시계열이 된다.
과거의 충격이 누적되어 장기적으로도 영향이 남음
단위근의 유무에 따른 특성 비교
| 구분 | 단위근 있음 (φ = 1) | 단위근 없음 (|φ| < 1) |
|---|---|---|
| 평균 | 시간에 따라 변함 | 일정함 |
| 분산 | 시간에 따라 증가 | 일정함 |
| 충격 영향 | 장기적으로 누적 | 단기적, 곧 사라짐 |
| 예시 | 주가, 환율 | 기온, 소비량(계절 조정 후) |
단위근 제거: 차분(Differencing)
단위근이 존재하는 시계열은 차분을 통해 정상성을 확보할 수 있다.
Python 예시:
df["diff"] = df["value"].diff()
차분 후에는 평균과 분산이 안정되어 ARIMA와 같은 시계열 모델을 적용할 수 있다.
ADF (Augmented Dickey-Fuller) Test는 “시계열에 단위근이 존재하는가?”를 검정하는 통계적 방법이다.
| 항목 | 설명 |
|---|---|
| 귀무가설 (H₀) | 단위근 존재 → 비정상 시계열 |
| 대립가설 (H₁) | 단위근 없음 → 정상 시계열 |
| 판단 기준 | p-value < 0.05 → 귀무가설 기각 → 정상성 확보 |
| 결과 해석 | 의미 |
|---|---|
| p-value < 0.05 | 정상 시계열 (차분 불필요) |
| p-value ≥ 0.05 | 비정상 시계열 (차분 필요) |
from statsmodels.tsa.stattools import adfuller
adf_result = adfuller(df["Passengers"])
print(f"ADF Statistic: {adf_result[0]:.3f}")
print(f"p-value: {adf_result[1]:.4f}")
차분(Differencing)
비정상 시계열은 차분(differencing) 을 통해 정상 시계열로 변환할 수있다.
차분은 이전 시점의 값을 현재 시점에서 빼서, 변화량을 기반으로 한 새로운 시계열을 만든다.
| 차분 종류 | 수식 | 설명 |
|---|---|---|
| 1차 차분 | \( Y'_t = Y_t - Y_{t-1} \) | 추세(Trend) 제거 |
| 계절 차분 | \( Y''_t = Y_t - Y_{t-s} \) | 계절성(Seasonality) 제거 |
| 복합 차분 | 1차 차분 + 계절 차분 순차 적용 | 추세와 계절성이 모두 존재할 때 사용 |
# 1차 차분 (Trend 제거)
df["diff1"] = df["Passengers"].diff(periods=1)
# 계절차분 (Seasonal Difference): 계절성 제거
# 12는 월별 데이터에서 1년 주기(12개월) 를 의미
df["diff_seasonal"] = df["Passengers"].diff(periods=12)
# 복합 차분: 추세 + 계절성 모두 제거
df["diff_both"] = df["Passengers"].diff(periods=1).diff(periods=12)
변동성(분산) 안정화
시계열의 변동 폭이 일정하지 않은 경우, 로그 변환(Log Transform) 또는 Box--Cox 변환을 사용하여 분산을 안정화할 수 있다.
| 방법 | 수식 | 설명 |
|---|---|---|
| 로그 변환 | \( Y'_t = \log(Y_t) \) | 값이 커질수록 변동 폭이 커지는 경우 사용 |
| Box–Cox 변환 | \( Y'_t = \frac{Y_t^{\lambda} - 1}{\lambda} \) | 로그보다 일반화된 형태로, 통계적 안정화에 효과적 |
import numpy as np
df["log_passengers"] = np.log(df["Passengers"])
차분 전후 시각화
# File: 08_stationarity_differencing_practice.py
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
# 1. 데이터 로드 (AirPassengers 데이터셋)
# 이 데이터는 1949~1960년 국제 항공 여객 수 (월별, 단위: 1000명)
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv"
df = pd.read_csv(url, parse_dates=['Month'], index_col='Month')
df.columns = ['Passengers'] # 컬럼명 통일
print(df.head())
# 2. 정상성 검정 (ADF Test)
adf_result = adfuller(df["Passengers"])
print("ADF Statistic:", round(adf_result[0], 3))
print("p-value:", round(adf_result[1], 4))
if adf_result[1] < 0.05:
print("✅ 정상 시계열 (차분 불필요)")
else:
print("⚠️ 비정상 시계열 (차분 필요)")
# 3. 차분 수행
df["diff1"] = df["Passengers"].diff()
df["diff_seasonal"] = df["Passengers"].diff(12)
# 4. 시각화 비교
fig, axes = plt.subplots(3, 1, figsize=(10,8), sharex=True)
axes[0].plot(df["Passengers"], label="Original", color='blue')
axes[0].set_title("Original Time Series")
axes[0].legend()
axes[1].plot(df["diff1"], label="1st Difference", color='orange')
axes[1].set_title("1st Difference (Trend Removed)")
axes[1].legend()
axes[2].plot(df["diff_seasonal"], label="Seasonal Difference", color='green')
axes[2].set_title("Seasonal Difference (Period=12)")
axes[2].legend()
plt.tight_layout()
plt.show()
실행 결과
Passengers
Month
1949-01-01 112
1949-02-01 118
1949-03-01 132
1949-04-01 129
1949-05-01 121
ADF Statistic: 0.815
p-value: 0.9919
⚠️ 비정상 시계열 (차분 필요)
| 비교 항목 | 차이점 |
|---|---|
| 원본 시계열 | 추세가 존재하여 평균이 일정하지 않음 |
| 차분 시계열 | 평균이 일정해지고 진동 중심이 안정됨 → 정상성 확보 |
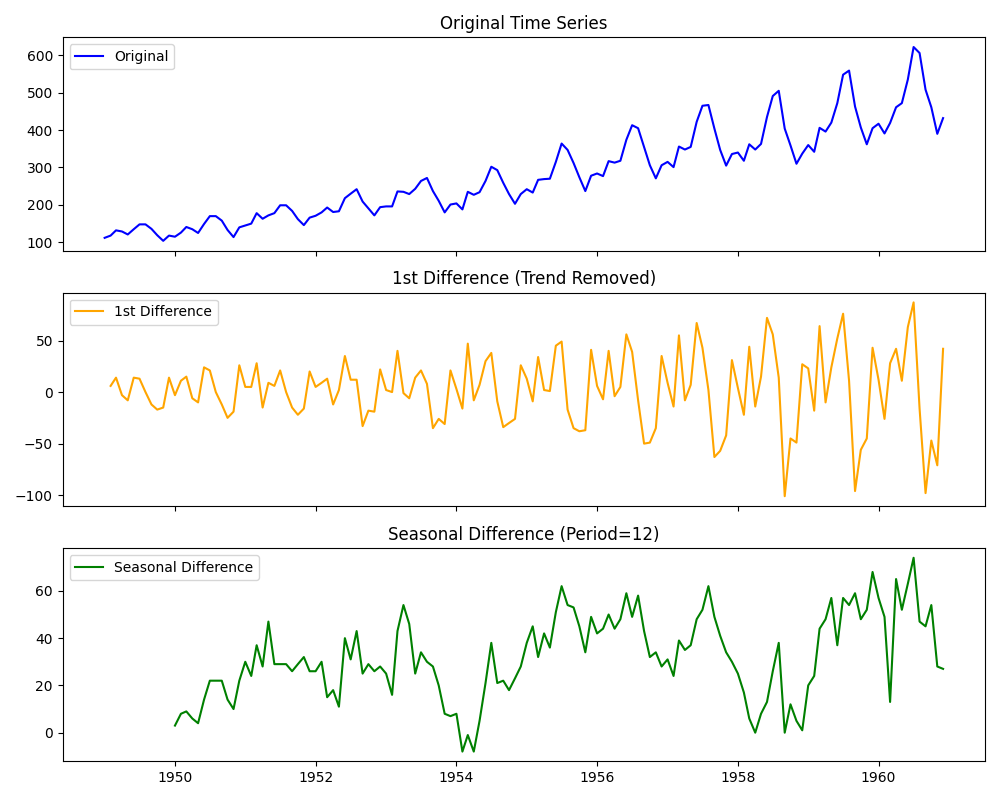
| 그래프 | 설명 |
|---|---|
| Original Time Series | 1949년부터 1960년까지의 국제 항공 여객 수를 나타낸 원본 시계열이다. 전반적으로 시간이 지남에 따라 여객 수가 꾸준히 증가하고 있으며, 연도마다 일정한 주기적 변동(계절성)이 반복된다. 이러한 패턴은 비정상 시계열(Non-stationary) 의 전형적인 특징이다. |
| 1st Difference (Trend Removed) | 1차 차분을 적용한 결과로, 전 시점과의 차이를 계산하여 추세(Trend) 성분이 제거되었다. 데이터의 평균이 일정한 중심을 기준으로 진동하는 형태로 바뀌며, 장기적인 증가 경향이 사라졌다. 그러나 여전히 주기적인 변동(계절성)은 남아 있다. |
| Seasonal Difference (Period=12) | 12개월 주기의 계절 차분을 적용한 결과로, 계절적 반복 패턴이 제거되었다. 이제 데이터는 특정 주기에 따른 진폭 변화가 감소하고, 평균이 일정하게 유지되는 정상 시계열(Stationary Series) 형태에 가까워졌다. |
ARIMA 계열 모델링
ARIMA(AutoRegressive Integrated Moving Average)는 비정상 시계열 데이터를 차분을 통해 정상화한 뒤, AR(자기회귀)과 MA(이동평균) 요소를 결합하여 예측하는 모델이다.
구성 요소
| 구성요소 | 의미 | 설명 |
|---|---|---|
| AR(p) | AutoRegressive | 과거 p개의 값이 현재 값에 영향을 미침 |
| I(d) | Integrated | d차 차분을 통해 비정상성을 제거 |
| MA(q) | Moving Average | 과거 q개의 오차항이 현재 값에 영향을 미침 |
파라미터 구조
| 모델 | 구성 | 설명 |
|---|---|---|
| \(ARIMA(p, d, q)\) | p: 자기회귀(AR) 차수d: 차분 횟수(정상성 확보 수준)q: 이동평균(MA) 차수 |
비계절형 시계열 모델 |
| \(SARIMA(p, d, q)(P, D, Q)\_{s}\) | (P, D, Q): 계절 성분 차수s: 주기(예: 12개월) |
계절성이 있는 시계열 모델 |
확장된 모델
| 모델 | 형태 | 설명 |
|---|---|---|
| \(ARIMA(p,d,q)\) | 기본형 | 추세 중심 |
| \(SARIMA(p,d,q)(P,D,Q)\_s\) | 계절형 | 계절성 주기 s 포함 |
| \(ARIMAX\) | ARIMA + 외생변수 | 외부 요인(x변수)을 함께 고려 |
| \(SARIMAX\) | SARIMA + 외생변수 | 계절성 + 외생변수 모델 |
모델 적합 프로세스
| 단계 | 절차 | 설명 |
|---|---|---|
| 1단계 | 데이터 전처리 | 결측치 처리, 로그 변환, 차분 등을 통해 데이터 정제 |
| 2단계 | 정상성 확보 | ADF 검정, 차분 등을 이용하여정상 시계열로 변환 |
| 3단계 | 모수 추정 | ACF, PACF 플롯을 통해AR(p), MA(q) 차수 후보 탐색 |
| 4단계 | 모델 선택 | AIC/BIC 값이 가장 낮은모델을 선택 |
| 5단계 | 모델 적합 및 평가 | 학습 후 잔차의 자기상관 검정 (Ljung–Box Test)으로 적합성 확인 |
| 6단계 | 예측 및 신뢰구간 분석 | 향후 값 예측 및 불확실성(Confidence Interval) 시각화 |
실습 코드 예제
# File: 09_sarima_forecasting_example_v2.py
# SARIMA 모델을 이용한 항공 여객 수 예측 실습 (경고 제거 버전)
# ------------------------------------------------------------
# 이 예제는 AirPassengers 데이터셋을 사용하여
# 월별 항공 여객 수를 예측하는 SARIMA 모델을 실습하는 코드이다.
# ------------------------------------------------------------
from statsmodels.tsa.statespace.sarimax import SARIMAX
import pandas as pd
import matplotlib.pyplot as plt
# ------------------------------------------------------------
# (1) 데이터 로드 및 전처리
# ------------------------------------------------------------
# AirPassengers 데이터셋: 1949~1960년 국제 항공 여객 수 (월별)
# 데이터 출처: https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv"
# CSV 파일을 불러오며, 'Month' 열을 날짜(Datetime)로 변환하고
# 이를 인덱스로 설정하여 시계열 형태로 구성
df = pd.read_csv(url, parse_dates=['Month'], index_col='Month')
# 컬럼명을 'Passengers'로 변경 (기존 컬럼명: 'Passengers'와 동일하지만 명시적으로 지정)
df.columns = ['Passengers']
# 인덱스 주기(frequency) 명시
# "MS"는 Month Start (매월 1일) 주기를 의미하며,
# statsmodels에서 주기 경고(ValueWarning)를 제거하기 위해 반드시 설정 필요
df = df.asfreq('MS') # 또는 df.index.freq = 'MS' 도 가능
# 데이터 확인 (앞부분 5개 행)
print(f"✅ Data frequency set to: {df.index.freqstr}")
print(df.head())
# ------------------------------------------------------------
# (2) SARIMA 모델 정의
# ------------------------------------------------------------
# SARIMA(p, d, q) (P, D, Q, s)
#
# ─ 비계절(Non-seasonal) 차수: order = (p, d, q)
# • p (AR order): 비계절 자기회귀 차수
# - 현재 시점 y_t가 과거의 y_{t-1}, y_{t-2}, ... y_{t-p}까지
# 몇 단계의 "값"에 의존하는지
# - p가 크면 과거 값들을 많이 참조 → 과적합 위험 ↑, PACF 절단점으로 대략 판단
# • d (Integration, differencing): 비계절 차분 횟수
# - 추세(비정상성) 제거를 위해 몇 번 차분할지 (보통 0 또는 1, 드물게 2)
# - 과도한 차분은 정보 손실/과분산 유의
# • q (MA order): 비계절 이동평균 차수
# - 현재 시점 y_t가 과거의 오차(잔차) e_{t-1}, e_{t-2}, ... e_{t-q}에
# 얼마만큼 의존하는지
# - q는 ACF 절단점으로 대략 판단
#
# ─ 계절(Seasonal) 차수: seasonal_order = (P, D, Q, s)
# • P (Seasonal AR order): 계절 자기회귀 차수
# - y_t가 계절 간격 s만큼 떨어진
# 과거 값(y_{t-s}, y_{t-2s}, …, y_{t-Ps})에 의존하는 정도
# - 예) s=12(월별 데이터)일 때, 1년 전/2년 전 같은 달의 값 의존
# • D (Seasonal differencing): 계절 차분 횟수
# - 계절적 평균 이동을 제거하기 위해 몇 번 계절 차분할지 (보통 0 또는 1)
# - D=1이면 ∇_s y_t = y_t − y_{t−s} (예: 이번 달 − 작년 같은 달)
# • Q (Seasonal MA order): 계절 이동평균 차수
# - 현재 y_t가 계절 간격 s로 떨어진 과거 오차(e_{t-s}, e_{t-2s}, …)에
# 의존하는 정도
# • s (Seasonal period): 계절 주기 길이
# - 월별 데이터의 연간 주기: s=12
# - 분기 데이터의 연간 주기: s=4
# - 일별 데이터의 주간 주기: s=7 등
#
# ─ 기타 옵션
# • enforce_stationarity=False
# - 모수 추정 시 “정상성(Stationarity) 제약”을 강제로 두지 않음
# - 데이터가 약간 비정상이어도 추정이 수렴하도록 유연성 부여
# • enforce_invertibility=False
# - “가역성(Invertibility) 제약”을 강제로 두지 않음
# - MA 성분이 경계에 가까운 경우에도 추정 허용(수렴성/안정성 트레이드오프)
#
# 예시: (1,1,1)(1,1,1,12)는
# → 비계절 AR(1) + 비계절 차분 1회(d=1) + 비계절 MA(1)
# → 12개월 주기의 계절 AR(1) + 계절 차분 1회(D=1) + 계절 MA(1)
# → 즉, 추세와 12개월 계절성이 모두 존재한다고 보고 이를 동시에 모형화
non_seasonal_order = (1, 1, 1) # (p, d, q)
seasonal_order = (1, 1, 1, 12) # (P, D, Q, s) ← 월별 데이터의 연간 주기
model = SARIMAX(
endog=df["Passengers"], # 종속변수 (시계열)
order=non_seasonal_order, # 비계절 차수 (p, d, q)
seasonal_order=seasonal_order, # 계절 차수 (P, D, Q, s)
enforce_stationarity=False, # 정상성 강제 X (경계 모수 허용)
enforce_invertibility=False, # 가역성 강제 X (경계 모수 허용)
)
# ------------------------------------------------------------
# (3) 모델 학습 (Fitting)
# ------------------------------------------------------------
# 모델 학습을 수행하면 내부적으로 MLE(Maximum Likelihood Estimation)를 통해
# AR, MA, 계절 항의 계수를 추정함
result = model.fit()
# ------------------------------------------------------------
# 결과 요약 출력 (모델 통계 요약표)
# ------------------------------------------------------------
# .summary() 출력 항목 주요 해석:
#
# [1] AIC (Akaike Information Criterion)
# - 모델의 적합도와 복잡도(파라미터 수)를 동시에 고려하는 지표
# - 값이 작을수록 데이터에 더 잘 맞고 과적합 위험이 낮음
# - 여러 모델 비교 시, AIC가 가장 작은 모델 선택
#
# [2] BIC (Bayesian Information Criterion)
# - AIC와 유사하지만, 복잡한 모델에 더 강한 패널티 부여
# - 데이터가 많을 때 BIC가 더 보수적인 모델을 선호함
# - 역시 값이 작을수록 좋은 모델
#
# [3] coef (Coefficient)
# - 각 AR, MA, Seasonal, Trend 항의 추정 계수(모델 파라미터)
# - 계수의 부호(+, -)로 변수의 영향 방향을 해석할 수 있음
#
# [4] std err (Standard Error)
# - 해당 계수의 추정치가 얼마나 불확실한지 나타냄
# - 작을수록 신뢰도 높은 추정 (즉, 변동성 적음)
#
# [5] z (z-statistic)
# - 계수 유의성 검정 통계량 (계수 / 표준오차)
# - |z| 값이 크면, 계수가 통계적으로 유의할 가능성이 높음
#
# [6] P>|z| (p-value)
# - 유의확률: 귀무가설(H0: 계수=0)을 기각할 확률
# - p < 0.05 → 해당 계수가 유의하게 0이 아님 (즉, 유효한 변수)
#
# [7] Ljung-Box (Q)
# - 잔차가 백색잡음(독립적)인지 검정
# - p > 0.05 → 잔차에 자기상관 없음 → 모델 적합 양호
#
# [8] Jarque-Bera (JB)
# - 잔차의 정규성(평균0, 대칭성)을 검정
# - p > 0.05 → 정규분포 가정 만족
#
# [9] Heteroskedasticity (H)
# - 잔차의 등분산성 여부 판단
# - 값이 1에 가까울수록 등분산(좋음)
#
# [10] Durbin–Watson
# - 잔차의 자기상관(특히 1차 자기상관) 여부 점검
# - 2에 가까울수록 자기상관 없음 (1 미만: 양의 상관, 3 이상: 음의 상관)
#
# 전체적으로:
# → AIC/BIC가 작고, 잔차 진단(Ljung-Box, JB, H, DW)이 양호하면
# 모델이 데이터 패턴을 잘 설명한다고 해석할 수 있음.
#
print(result.summary())
# ------------------------------------------------------------
# (4) 미래 12개월(1년) 예측
# ------------------------------------------------------------
# 향후 12개월 데이터를 예측 (forecast)
forecast = result.get_forecast(steps=12)
# 예측 평균값
forecast_mean = forecast.predicted_mean
# 예측 구간 (95% 신뢰구간)
forecast_ci = forecast.conf_int()
# ------------------------------------------------------------
# (5) 예측 결과 시각화
# ------------------------------------------------------------
plt.figure(figsize=(10, 5))
# 실제 관측값 (1949~1960)
plt.plot(df.index, df["Passengers"], label="Observed", color='blue')
# 예측된 평균값 (1961~1962)
plt.plot(forecast_mean.index, forecast_mean, label="Forecast", color='orange')
# 예측 신뢰구간 (Confidence Interval)
plt.fill_between(
forecast_ci.index,
forecast_ci.iloc[:, 0],
forecast_ci.iloc[:, 1],
color='orange',
alpha=0.3,
label="Confidence Interval"
)
# 그래프 제목 및 레이블
plt.title("SARIMA Forecast for AirPassengers (1 year ahead)", fontsize=13)
plt.xlabel("Year")
plt.ylabel("Number of Passengers (in thousands)")
# 범례 및 레이아웃 조정
plt.legend()
plt.tight_layout()
plt.show()
실행 결과
✅ Data frequency set to: MS
Passengers
Month
1949-01-01 112
1949-02-01 118
1949-03-01 132
1949-04-01 129
1949-05-01 121
SARIMAX Results
=========================================================================
Dep. Variable: Passengers No. Observations: 144
Model: SARIMAX(1, 1, 1)x(1, 1, 1, 12) Log Likelihood -456.103
Date: Fri, 17 Oct 2025 AIC 922.205
Time: 12:24:02 BIC 936.016
Sample: 01-01-1949 HQIC 927.812
- 12-01-1960
Covariance Type: opg
=========================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------
ar.L1 -0.2298 0.401 -0.573 0.567 -1.016 0.557
ma.L1 -0.0987 0.374 -0.264 0.792 -0.832 0.634
ar.S.L12 -0.5460 0.299 -1.825 0.068 -1.133 0.041
ma.S.L12 0.3959 0.352 1.125 0.261 -0.294 1.086
sigma2 140.2945 17.997 7.795 0.000 105.020 175.569
=========================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 5.42
Prob(Q): 0.95 Prob(JB): 0.07
Heteroskedasticity (H): 2.51 Skew: 0.12
Prob(H) (two-sided): 0.01 Kurtosis: 4.03
=========================================================================
| 평가 항목 | 설명 |
|---|---|
| AIC / BIC | 모델의 적합도를 비교하는 지표. 값이 낮을수록 좋은 모델을 의미함 |
| 잔차 자기상관 (Ljung–Box Test) |
잔차가 백색잡음(white noise)인지 확인. 비상관이면 모델이 적절함 |
| 잔차 정규성 검정 (Q–Q Plot) |
잔차가 정규분포를 따르는지 시각적으로 확인 |
| 예측 신뢰구간 (Confidence Interval) |
예측의 불확실성을 시각적으로 표현. 신뢰구간이 좁을수록 예측이 안정적임 |
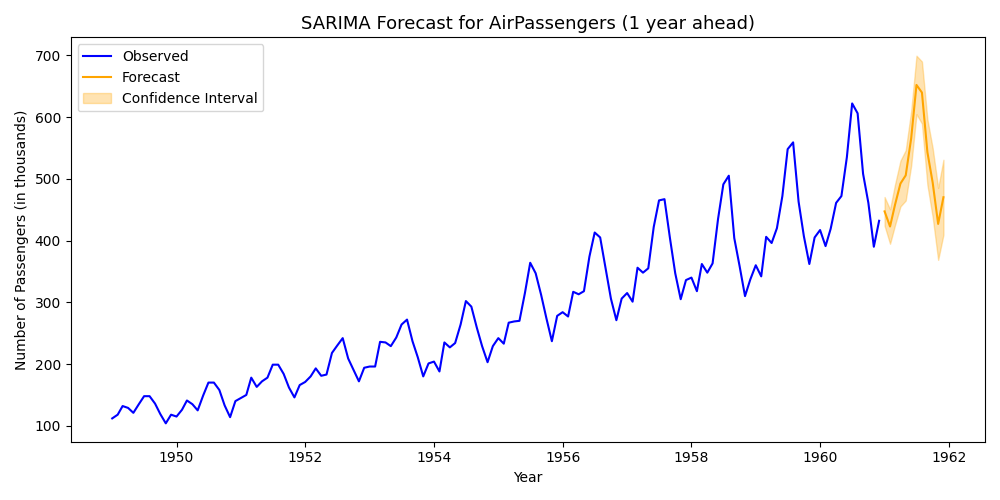
대안 모델과 최신 도구
시계열 분석은 더 이상 단순히 ARIMA 계열 모델에 국한되지 않는다.
데이터의 양과 다양성이 급격히 증가함에 따라, 복잡한 패턴과 다중 계절성을 반영할 수 있는 고급 예측 모델들이 널리 활용되고 있다.
이 절에서는 실제 프로젝트에서 자주 사용되는 대안 모델들을 소개하고, 각각의 특징과 활용 시 고려 사항을 설명한다.
Prophet (by Facebook / Meta)
Prophet은 Facebook에서 개발한 시계열 예측 도구로, 추세(Trend), 계절성(Seasonality), 이벤트 효과(Holiday Effect)를 각각 독립적으로 모델링할 수 있도록 설계되었다.
선형 회귀 기반의 단순한 구조를 유지하면서도 휴일, 캠페인, 정책 변경 등 도메인 이벤트의 영향을 손쉽게 반영할 수 있다는 점에서 실무에서 매우 광범위하게 사용된다.
Prophet은 또한 결측치나 이상값에 비교적 강건하며, 직관적인 파라미터 설정과 시각화 기능을 제공한다. 다만, 긴 시계열 데이터(약 2년 이상)에서 가장 안정적인 성능을 보이며, 단기 데이터나 과도한 이벤트 추가 시 과적합 위험이 존재한다.
요약
-
추세와 계절성을 분리하여 구성
-
공휴일 효과나 외부 요인 반영 용이
-
Python과 R에서 쉽게 사용 가능
-
짧은 시계열 데이터에서는 과적합 주의
TBATS
TBATS는 Trigonometric, Box--Cox, ARMA, Trend, Seasonal의 약자로, 복수의 계절성(Multiple Seasonality) 과 비정상 주기를 다룰 수 있도록 고안된 고급 통계 모델이다.
예를 들어, 일 단위 데이터에서 주간(7일)과 연간(365일) 주기가 동시에 존재하는 경우, TBATS는 각 주기를 트리거노메트릭(삼각함수) 기반으로 효율적으로 표현한다.
TBATS는 Box--Cox 변환을 통해 분산을 안정화하고, ARMA 구성요소로 단기적 변동을 모델링할 수 있다.
단점으로는 계산 복잡도가 높고, 대규모 데이터셋에서는 훈련 속도가 느릴 수 있다.
요약
-
다중 계절성 모델링에 적합
-
비정상적, 불규칙한 주기 데이터 처리 가능
-
계산량이 많고 해석이 다소 어려움
LSTM (Long Short-Term Memory)
LSTM은 순환 신경망(RNN)의 일종으로, 시계열 데이터의 장기 의존 관계(Long-term dependency)를 학습하는 데 특화되어 있다.
전통적인 통계 모델과 달리 비선형 패턴을 학습할 수 있어, 복잡한 시계열(예: 주가, 센서 데이터, 사용자 행동 로그) 에서 높은 성능을 보인다.
LSTM은 다변량(Multivariate) 시계열 입력을 자연스럽게 처리할 수 있으며, 외부 요인(날씨, 이벤트 등)을 피처로 함께 투입할 수 있다.
다만, 모델 학습에 많은 데이터와 GPU 자원이 필요하며, 모델의 해석력(interpretability)이 낮다는 단점이 있다.
요약
-
장기 패턴 및 비선형 관계 학습 가능
-
다변량 입력 및 외부 요인 반영 가능
-
대규모 데이터에 적합, 해석 어려움
Temporal Convolutional Networks (TCN)
TCN은 합성곱 신경망(CNN)을 시계열에 적용한 모델로, 순차적 데이터의 순서를 유지한 채 병렬 처리가 가능하다.
이는 전통적인 RNN보다 학습 속도가 빠르며, 멀티스텝 예측(multi-step forecasting) 에 유리하다.
TCN은 긴 시점 간의 의존 관계를 Dilated Convolution을 통해 포착하며, 모델의 안정성과 효율성을 모두 확보한다.
그러나 불규칙한 샘플링 간격이나 짧은 시계열에서는 LSTM 대비 성능이 낮을 수 있다.
요약
-
1D 합성곱 기반 시계열 모델
-
LSTM보다 빠르고 병렬 학습 가능
-
긴 의존 관계 학습에 강점, 하이퍼파라미터 조정은 복잡
Transformer 기반 시계열 모델
최근에는 NLP 분야에서 성공적인 성과를 보인 Transformer 구조가 시계열 예측에도 적용되고 있다.
대표적인 예로 Informer, Temporal Fusion Transformer(TFT), FEDformer 등이 있으며, 이들은 Attention 메커니즘을 통해 시점 간의 중요도를 동적으로 학습한다.
이 모델들은 다변량 시계열(multivariate time series)에 특히 강하며, 외부 변수(날씨, 이벤트, 정책 등) 를 함께 입력받아 고정된 주기를 넘어선 복잡한 패턴을 학습할 수 있다.
정확도와 확장성은 높지만, 학습 데이터와 GPU 자원이 많이 필요하고 모델 해석이 어렵다는 한계가 있다.
요약
-
Attention 기반 시계열 학습 구조
-
다변량 데이터 및 외부 변수 반영 가능
-
정확도 높지만 계산 비용 큼, 해석 어려움