상관 및 회귀 분석
- 강의자료 다운로드: click me
데이터 과학에서 변수들 간의 관계를 파악하는 것은 매우 중요한 출발점이다. 특히 하나의 변수가 다른 변수와 어떤 방식으로 관련되어 있는지를 이해하면, 단순한 데이터 관찰을 넘어 패턴 발견과 예측으로 나아갈 수 있다. 이번 주차에서는 이러한 관계를 수치적으로 표현하고, 모델링할 수 있는 두 가지 핵심 기법인 상관 분석(Correlation Analysis) 과 회귀 분석(Regression Analysis) 을 다룬다.
먼저, 상관 분석을 통해 두 변수 간의 선형적 관계의 방향과 강도를 수치로 나타내는 방법을 학습한다. 대표적인 지표인 피어슨 상관계수를 활용하여 변수 간의 관계를 정량적으로 파악하고, 상관행렬 및 히트맵 시각화를 통해 데이터의 전반적인 구조를 탐색한다.
회귀 분석에서는 단순 회귀와 다중 회귀 모델을 통해 변수 간의 관계를 수학적 함수로 모델링하고, 이를 기반으로 미래 값을 예측하거나 관계의 영향력을 해석하는 방법을 다룬다. 단순 회귀분석을 통해 하나의 독립변수가 종속 변수에 미치는 영향을 분석하고, 다중 회귀분석을 통해 여러 요인이 동시에 결과에 어떤 영향을 주는지 살펴본다. 또한 잔차 분석을 통해 모델의 적합도를 평가하고, 실제 데이터 분석에서 주의해야 할 해석상의 함정도 함께 짚어본다.
이번 주차를 통해 데이터셋에서 변수 간의 상관관계를 파악하고, 이를 바탕으로 회귀 모델을 구축·해석할 수 있는 능력을 기르게 될 것이다. 이는 이후 시계열 분석, 텍스트 분석 등 보다 복잡한 데이터 분석 주제로 나아가기 위한 핵심 기초가 된다.
상관 분석
상관의 개념
상관은 두 변수가 함께 변하는 정도를 수치로 나타낸 것이다. 다시 말하면 상관이란 두 변수가 서로 얼마나 함께 변하는지를 수치로 표현한 것이다. 즉, 한 변수가 변할 때 다른 변수가 같은 방향으로 움직이는지, 혹은 반대 방향으로 움직이는지, 또는 서로 관계가 없는지를 알아보는 것이다.
- 양의 상관 → 두 변수가 함께 증가
- 음의 상관 → 한 변수가 증가할 때 다른 변수는 감소
- 0에 가까운 상관 → 선형적 관계가 거의 없음
예를 들어, 학생들의 공부 시간과 시험 점수를 생각해보자.
보통 공부 시간이 늘어날수록 시험 점수도 함께 올라가는 경향이 있다. 이런 경우 두 변수는 양의 상관(positive correlation) 을 가진다고 한다. 두 변수의 값이 나란히 증가하므로, 상관계수 값도 1에 가까운 큰 양수가 된다.

반대로, 운동 시간과 체중 사이의 관계를 생각해보자. 일반적으로 운동 시간이 늘어나면 체중은 감소하는 경향이 있다. 이런 경우는 음의 상관(negative correlation) 에 해당하며, 한 변수가 증가할 때 다른 변수는 줄어드는 형태다. 상관계수 값은 -1에 가까운 음수가 된다.

마지막으로, 신발 사이즈와 수학 점수처럼 서로 관련이 없는 변수들도 있다. 이런 경우에는 두 변수의 변화가 서로 영향을 주지 않기 때문에 상관계수가 0에 가까운 값을 나타낸다. 이는 선형적인 관계가 거의 없다는 뜻이다.

요약하자면, 상관은 단순히 두 변수의 증감 패턴이 같은지(양의 상관), 반대인지(음의 상관), 무관한지(상관 없음) 를 수치로 보여주는 개념이다. 이를 통해 데이터 간의 관계를 직관적으로 파악할 수 있으며, 이후 회귀분석이나 예측 모델링의 기초가 된다.
피어슨 상관계수 (Pearson Correlation Coefficient)
두 변수 사이의 선형적 관계를 수치로 표현할 때 가장 널리 사용되는 지표는 피어슨 상관계수(Pearson Correlation Coefficient) \(r\) 이다.
상관계수를 이해하기 위해서는 먼저 공분산(Covariance) 의 개념을 알아야 한다. 공분산은 두 변수가 서로 함께 변하는 정도를 나타내는 값이다.
예를 들어, 공부 시간과 시험 점수를 살펴보면, 공부 시간이 늘어날 때 점수도 함께 증가하는 경향이 있다면 두 변수는 같은 방향으로 움직인다고 볼 수 있다. 이런 경우 공분산 값은 양수가 된다. 반대로, 운동 시간과 체중처럼 한 변수가 커질 때 다른 변수가 줄어드는 관계라면, 두 변수는 반대 방향으로 움직인다고 볼 수 있으며 공분산 값은 음수가 된다.
공분산의 기본 수식은 다음과 같다.
- \((x_i - \bar{x})\): X 변수의 각 값이 평균에서 얼마나 떨어져 있는지
- \((y_i - \bar{y})\): Y 변수의 각 값이 평균에서 얼마나 떨어져 있는지
- 두 편차를 곱했을 때 양수 → 같은 방향으로 변함
- 두 편차를 곱했을 때 음수 → 반대 방향으로 변함
예를 들어, 아래와 같이 3명의 학생에 대한 공부 시간(X) 과 시험 점수(Y) 가 있다고 하자.
| 학생 | 공부 시간 X | 시험 점수 Y |
|---|---|---|
| A | 1 | 2 |
| B | 2 | 3 |
| C | 3 | 6 |
먼저, 각 변수의 평균을 구한다.
- \(\bar{X} = \frac{1+2+3}{3} = 2\)
- \(\bar{Y} = \frac{2+3+6}{3} = 3.67\)
각 데이터에서 평균을 뺀 편차를 구하고, X와 Y의 편차를 서로 곱해서 모두 더한다.
| 학생 | X | Y | X−X̄ | Y−Ȳ | (X−X̄)(Y−Ȳ) |
|---|---|---|---|---|---|
| A | 1 | 2 | -1 | -1.67 | 1.67 |
| B | 2 | 3 | 0 | -0.67 | 0.00 |
| C | 3 | 6 | 1 | 2.33 | 2.33 |
이제 이 값들을 모두 더해서 데이터 개수로 나눈다.
공분산이 양수이므로, X와 Y는 같은 방향으로 함께 움직이는 경향이 있음을 알 수 있다. 즉, 공부 시간이 늘어날수록 시험 점수도 증가하는 경향이 있다는 뜻이다.
만약 반대로, X가 증가할 때 Y가 감소하는 데이터였다면 공분산 값은 음수가 되었을 것이다. 또한 X와 Y가 전혀 관계가 없는 경우, 공분산 값은 0에 가까워진다.
이처럼 공분산은 두 변수의 방향성을 알 수 있는 중요한 지표이지만, 값의 크기가 변수의 단위와 크기에 따라 달라진다는 단점이 있다. 예를 들어, 공부 시간을 ‘시간’ 단위로 측정하느냐 ‘분’ 단위로 측정하느냐에 따라 공분산 값이 커질 수도, 작아질 수도 있다. 이런 이유로 서로 다른 단위를 가진 변수들 간의 관계를 공정하게 비교하기 어렵다.
그래서 등장한 것이 바로 피어슨 상관계수이다. 피어슨 상관계수는 공분산을 각 변수의 표준편차로 나누어 정규화함으로써, -1과 1 사이의 표준화된 지표를 제공한다. 즉, 공분산이 관계의 “방향과 크기”를 보여준다면, 피어슨 상관계수는 이를 단위와 크기에 상관없이 비교 가능하게 만든 값이다.
이는 두 변수가 얼마나 함께 증가하거나 감소하는 경향이 있는지를 정량적으로 나타내며, 다음과 같은 수식으로 정의된다.
위 식을 보면, 각 데이터에서 평균을 뺀 값 \((x_i - \bar{x})\)과 \((y_i - \bar{y})\)를 곱해 모두 더하고, 이를 각 변수의 표준편차로 나누는 형태임을 알 수 있다. 즉, 공분산을 각 변수의 표준편차로 정규화한 값이라고 이해할 수 있다.
- \(r\)의 값은 항상 \(-1\)과 \(1\) 사이에 존재한다.
- \(r = 1\): 두 변수가 완벽하게 같은 방향으로 선형적으로 증가 (완전한 양의 상관)
- \(r = -1\): 한 변수가 증가할 때 다른 변수가 완벽하게 감소하는 관계 (완전한 음의 상관)
- \(r = 0\): 두 변수 간에 선형적인 상관관계가 없음
예를 들어, 공부 시간과 시험 점수의 관계처럼 하나가 증가하면 다른 것도 비례해서 증가한다면 \(r\)은 1에 가깝다. 반대로, 운동 시간과 체중의 관계처럼 한쪽이 증가하면 다른 쪽이 일정하게 감소하는 경우 \(r\)은 -1에 가깝게 나타난다. 그리고 신발 사이즈와 수학 점수처럼 아무런 관련이 없는 경우에는 \(r\) 값이 0에 가까워진다.
⚠️ 주의할 점 상관계수는 단지 “같이 움직이는 정도”를 나타낼 뿐, 인과관계를 의미하지 않는다. 예를 들어, 아이스크림 판매량과 익사 사고 건수는 여름에 모두 증가하므로 상관계수가 높게 나올 수 있지만, 이는 아이스크림이 사고를 유발했다는 뜻이 아니다. 이런 경우처럼 제3의 요인(계절)이 존재할 수 있으므로, 상관계수 해석 시에는 항상 맥락을 함께 고려해야 한다.
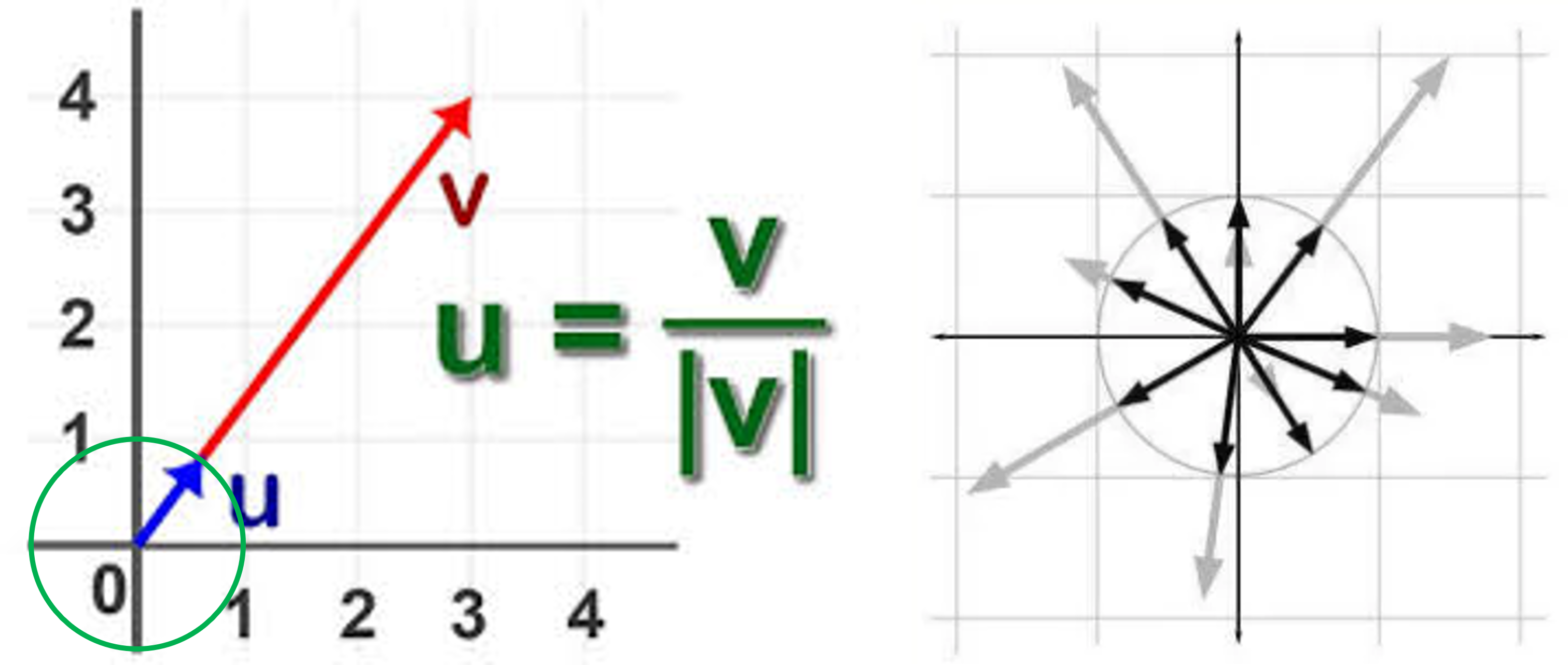
코사인 유사도 (Cosine Similarity)
두 벡터 간의 유사도를 측정할 때 널리 사용되는 지표 중 하나가 코사인 유사도(Cosine Similarity) 이다. 피어슨 상관계수가 데이터의 평균을 제거하고 선형적 동조성을 측정하는 데 초점을 맞추는 반면, 코사인 유사도는 두 벡터의 크기와 단위를 무시하고, 방향(각도) 만을 기준으로 유사성을 계산한다.
즉, 두 벡터가 같은 방향을 가리킨다면 코사인 유사도는 1에 가깝고, 서로 반대 방향을 가리키면 -1, 그리고 서로 직각(무관)이면 0에 가까운 값을 가진다.
수식
- \(x \cdot y\) : 두 벡터의 내적 (dot product)
- \(\|x\|\), \(\|y\|\) : 각 벡터의 크기(노름, L2 norm)
코사인 유사도는 L2 Norm으로 정규화 하기 때문에 단위에 영향을 받지 않으며, 벡터의 크기보다는 방향에 초점을 둔다.
특징 및 해석
- 값의 범위: \([-1, 1]\)
- \(1\) → 완전히 같은 방향 (두 벡터가 평행하고 방향도 동일)
- \(0\) → 직각 관계, 서로 관련 없음
- \(-1\) → 완전히 반대 방향
예시
다음 두 벡터를 생각해보자.
- 내적: \(x \cdot y = 1×2 + 2×4 + 3×6 = 28\)
- \(\|x\| = \sqrt{1^2+2^2+3^2} = \sqrt{14}\)
- \(\|y\| = \sqrt{2^2+4^2+6^2} = \sqrt{56}\)
두 벡터가 정확히 같은 방향을 가리키기 때문에 코사인 유사도는 1이다.
반면 다음과 같이 상수항이 더해진 경우를 보자.
이 경우 두 벡터는 방향이 약간 달라지므로 코사인 유사도는 1보다 작은 값이 나온다.
하지만 각 값에서 평균을 빼고 계산하는 피어슨 상관계수는 여전히 1을 유지한다.
이 차이가 바로 코사인 유사도 vs 피어슨 상관계수의 핵심이다.
주의점
-
코사인 유사도는 데이터의 이동(shift) 에 민감하다.
즉, 모든 값에 일정한 상수를 더하면 벡터의 방향이 바뀌어 유사도가 달라질 수 있다.
반면 피어슨 상관계수는 평균을 제거하기 때문에 이동에 영향을 받지 않는다.
-
코사인 유사도는 고차원 벡터(예: 문장 임베딩, 사용자-아이템 벡터)에서 두 벡터의 방향적 유사성을 측정할 때 유용하다.
크기나 단위가 달라도 벡터가 같은 방향을 가리킨다면 높은 유사도를 가진다.
실습 1: 완전 선형 관계(스케일만 다름)
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10]) # x와 완전 선형 관계 (배수)
pearson_r = np.corrcoef(x, y)[0, 1]
cos_sim = cosine_similarity([x], [y])[0, 0]
print("피어슨 상관계수:", pearson_r)
print("코사인 유사도:", cos_sim)
- 출력결과
실행결과
피어슨 상관계수: 1.0
코사인 유사도: 0.9999999999999999
해석: 크기만 달라도 선형 패턴과 방향이 동일하므로 두 값 모두 1에 가깝다.
실습 2: 상수항(평행 이동) 추가
x = np.array([1, 2, 3, 4, 5])
y = x + 100 # 평균이 크게 이동
pearson_r = np.corrcoef(x, y)[0, 1]
cos_sim = cosine_similarity([x], [y])[0, 0]
print("피어슨 상관계수:", pearson_r)
print("코사인 유사도:", cos_sim)
- 출력결과
실행결과
피어슨 상관계수: 1.0
코사인 유사도: 0.9786043735886338
해석:
-
피어슨: 평균을 뺀 뒤 보는 지표라서 “형태가 같은가?”만 보며 1.0 유지
-
코사인: 평균 이동으로 각도가 미세하게 변해 1에서 멀어진다
언제 무엇을 쓸까?
| 구분 | 피어슨 상관계수 | 코사인 유사도 |
|---|---|---|
| 목적 | 통계적 상관 (공분산 기반) | 벡터 의미 유사성 (방향 기반) |
| 데이터 특성 | 연속형 변수, 선형적 관계 가정 | 고차원 임베딩(문장/문서/이미지), sparse 벡터 |
| 사용 상황 | 변수 간 관계 탐색, 회귀 전 상관 검토 | 검색/추천 시스템, 최근접 이웃 탐색, 문장 의미 비교 |
| 값의 해석 | -1~1, 평균 제거 후 선형 관계 중심 | -1~1 (주로 0~1), 크기 무시하고 방향 중심 |
| 민감성 | 평균 이동(shift)에 영향 없음 | 평균 이동(shift)에 민감 |
| 주 사용 분야 | 통계, 데이터 분석, 회귀 모델링 | 자연어 처리, 추천 시스템, 벡터 검색, 임베딩 기반 모델 |
주의사항
-
상관 ≠ 인과: 높은 피어슨 값이 원인-결과를 의미하진 않는다.
-
비선형 관계: 피어슨은 선형성에 민감. 비선형이라면 다른 분석방법을 생각해야 함.
-
스케일 & 평균 처리:
-
피어슨은 평균 중심화가 내장
-
코사인은 크기를 무시하지만 평균 이동에는 민감 → 필요 시 중앙값/평균 보정 고려
-
-
희소 벡터(예: TF–IDF): 코사인이 안정적이고 빠르게 동작하는 편
상관행렬 및 히트맵 시각화
10개 변수간의 상관계수를 확인하는 코드
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# 랜덤 시드 고정
np.random.seed(42)
n_samples = 200
# 기본 변수 3개를 먼저 생성
X1 = np.random.normal(50, 10, n_samples)
X2 = X1 * 0.6 + np.random.normal(0, 5, n_samples) # X1과 상관 있는 변수
X3 = np.random.normal(30, 5, n_samples)
X4 = X2 * -0.5 + np.random.normal(0, 5, n_samples) # X2와 음의 상관
X5 = X3 + np.random.normal(0, 2, n_samples)
X6 = np.random.normal(100, 20, n_samples)
X7 = X1 * 0.3 + X3 * 0.4 + np.random.normal(0, 10, n_samples)
X8 = np.random.uniform(0, 1, n_samples)
X9 = X5 * 1.2 + np.random.normal(0, 3, n_samples)
X10 = np.random.normal(0, 1, n_samples)
# 데이터프레임 생성
df_multi = pd.DataFrame({
'X1': X1,
'X2': X2,
'X3': X3,
'X4': X4,
'X5': X5,
'X6': X6,
'X7': X7,
'X8': X8,
'X9': X9,
'X10': X10
})
# 상관행렬 계산
corr_matrix = df_multi.corr()
# 히트맵 시각화
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt=".2f", square=True)
plt.title("Heatmap of Correlation Matrix (10 Variables)")
plt.tight_layout()
plt.show()
실행결과
위 코드를 실행하면, 10개의 변수를 포함한 데이터셋에 대해 계산된 상관행렬(Correlation Matrix) 을 히트맵(heatmap) 형태로 시각화한 결과가 나타난다.
히트맵은 각 변수 쌍 사이의 피어슨 상관계수 값을 색상으로 표현한 것으로,
-
양의 상관(positive correlation) 값은 붉은색 계열,
-
음의 상관(negative correlation) 값은 파란색 계열,
-
0에 가까운 값은 흰색 또는 중간색으로 표시된다.
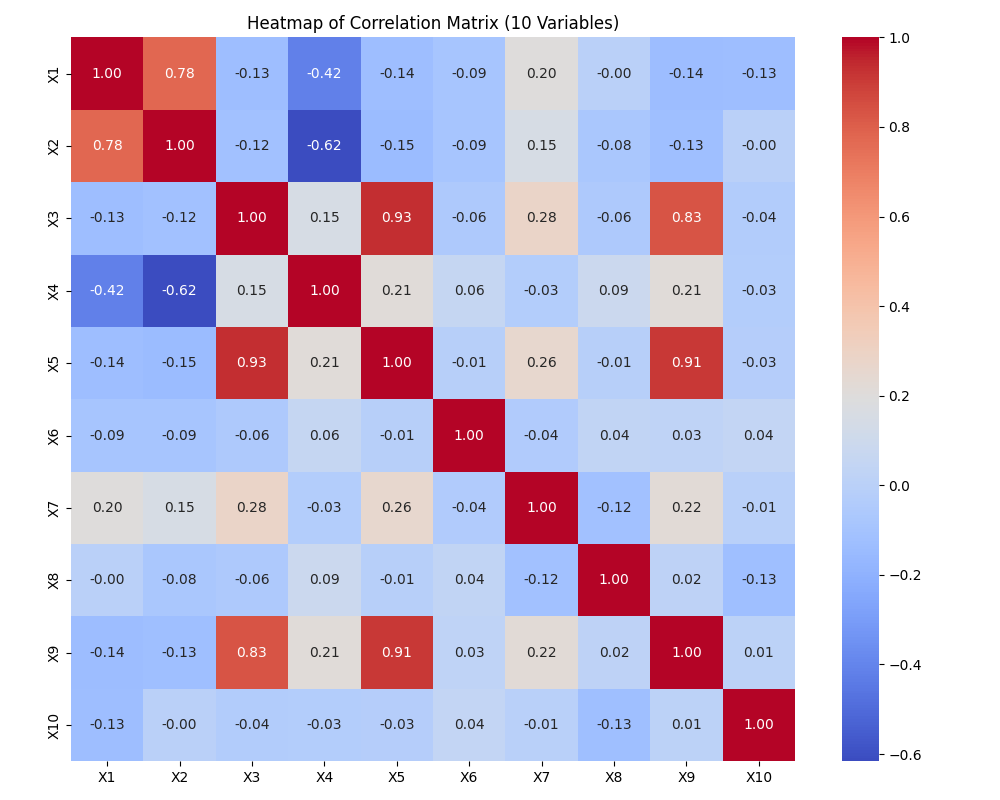
대각선에는 각 변수와 자기 자신 간의 상관계수 값이 1로 표시된다.
변수들 간에 인위적으로 상관 구조를 설정했기 때문에, 일부 변수 쌍은 0.6~0.8 수준의 높은 양의 상관을 보이고, 다른 변수 쌍은 -0.5 수준의 음의 상관을 보여 다양한 색상 패턴이 나타난다.
예를 들어, X1과 X2는 양의 상관 구조를 가지도록 생성되었기 때문에 히트맵에서도 이들의 교차 지점이 진한 붉은색으로 나타난다. 반면, X2와 X4는 음의 상관 구조를 가지므로 푸른색 영역으로 표시된다.
이러한 히트맵은 여러 변수 간의 관계를 한눈에 시각적으로 파악할 수 있게 해주며, 이후 회귀분석이나 차원 축소 등의 단계에서 변수 선택이나 다중공선성(multicollinearity) 점검에도 유용하게 활용할 수 있다.
Kaggle 데이터 분석 (주택 가격에 영향을 주는 요인 분석)
문제 개요
도시의 주택 가격은 여러 요인(예: 방 수, 인근 범죄율, 학교 수준, 공기 질 등)에 영향을 받는다. 이번 실습에서는 Kaggle의 Boston House Price 데이터셋을 사용하여 다음을 분석한다.
-
변수 간의 상관관계 분석
-
상관행렬 및 히트맵 시각화
-
주요 요인 탐색
-
데이터셋 다운로드: https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques/data
-
직접 다운로드 받기: click me
-
회원가입 및 로그인이 필요할 수 있음.
-
웹페이지 하단으로 이동하여
boston.csv다운로드 한다.
-
-
변수 설명
변수 설명 CRIM 마을별 1인당 범죄 발생률 ZN 25,000 평방피트(약 2323㎡) 이상의 대형 주택용 토지로 지정된 주거용 토지 비율 INDUS 마을별 비소매(non-retail) 상업 지역 비율 CHAS 찰스강과 접해 있는지 여부를 나타내는 더미 변수 (1: 접함, 0: 접하지 않음) NOX 대기 중 질소 산화물 농도 (1000만분의 1 단위) RM 주택당 평균 방 개수 AGE 1940년 이전에 지어진 자가주택의 비율 DIS 보스턴의 5개 주요 고용 중심지까지의 가중 거리 RAD 고속도로 접근성 지수 TAX 재산세율 (10,000달러당 세금액) PTRATIO 학생-교사 비율 B 흑인 인구 비율을 기반으로 계산된 지표. 식: 1000(Bk − 0.63)², 여기서 Bk는 흑인 인구 비율 LSTAT 하위 계층(저소득층) 인구의 비율(%) MEDV 자가주택의 중앙 가격 (단위: 1,000달러)
실습 단계
1) 데이터 불러오기 및 기본 확인
-
pandas로 CSV 불러오기 -
df.info(),df.describe(),df.isnull().sum()등으로 결측치/변수 유형 확인
2) 수치형 변수만 추출하여 상관행렬 계산
-
df.corr()사용 -
MEDV (자가주택의 중앙 가격)와의 상관계수를 내림차순 정렬하여 주요 요인 탐색
3) 히트맵 시각화
-
sns.heatmap으로 전체 상관행렬 (correlation matrix) 시각화 -
MEDV (자가주택의 중앙 가격)상관이 높은 상위 5개 변수 만 뽑아 별도 히트맵 생성
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# 1. 데이터 로드 및 기본 확인
DATA_PATH = "./boston.csv" # 파일명은 데이터셋에 따라 조정
if not os.path.exists(DATA_PATH):
raise FileNotFoundError(f"'{DATA_PATH}' 파일을 찾을 수 없습니다. 데이터를 다운로드하고 경로를 확인하세요.")
df = pd.read_csv(DATA_PATH)
print("데이터 크기:", df.shape)
print("\n컬럼 타입 요약:")
print(df.dtypes.value_counts())
print("\n결측치 상위 컬럼:")
print(df.isnull().sum().sort_values(ascending=False).head())
print("\n수치형 변수 기술통계 (상위 5):")
print(df.describe().T.head())
# 2. 수치형 변수만 상관행렬 계산
target_col = "MEDV"
if target_col not in df.columns:
raise KeyError(f"'{target_col}' 컬럼이 없습니다. 데이터셋을 확인하세요.")
num_df = df.select_dtypes(include=[np.number])
corr_all = num_df.corr(method="pearson")
target_corr = corr_all[target_col].drop(labels=[target_col]).sort_values(ascending=False)
top_feats = target_corr.head(10).index.tolist()
corr_top = corr_all.loc[top_feats + [target_col], top_feats + [target_col]]
print("\n{}와 상관 상위 10개 변수:".format(target_col))
print(target_corr.head(10))
# 3‑1. 전체 상관행렬 히트맵
plt.figure(figsize=(12, 10))
sns.heatmap(
corr_all,
cmap="coolwarm",
center=0,
square=True,
cbar=True,
xticklabels=False,
yticklabels=False
)
plt.title("Correlation Matrix (All Numeric Features)")
plt.tight_layout()
plt.show()
# 3‑2. 상위 변수 + Target 히트맵
plt.figure(figsize=(8, 6))
sns.heatmap(
corr_top,
cmap="coolwarm",
center=0,
square=True,
annot=True, fmt=".2f",
cbar=True
)
plt.title(f"Correlation Matrix (Top variables with {target_col})")
plt.tight_layout()
plt.show()
실행 결과
데이터 크기: (506, 14)
컬럼 타입 요약:
float64 12
int64 2
Name: count, dtype: int64
결측치 상위 컬럼:
CRIM 0
ZN 0
INDUS 0
CHAS 0
NOX 0
dtype: int64
수치형 변수 기술통계 (상위 5):
count mean std min 25% 50% 75% max
CRIM 506.0 3.613524 8.601545 0.00632 0.082045 0.25651 3.677083 88.9762
ZN 506.0 11.363636 23.322453 0.00000 0.000000 0.00000 12.500000 100.0000
INDUS 506.0 11.136779 6.860353 0.46000 5.190000 9.69000 18.100000 27.7400
CHAS 506.0 0.069170 0.253994 0.00000 0.000000 0.00000 0.000000 1.0000
NOX 506.0 0.554695 0.115878 0.38500 0.449000 0.53800 0.624000 0.8710
MEDV와 상관 상위 10개 변수:
RM 0.695360
ZN 0.360445
B 0.333461
DIS 0.249929
CHAS 0.175260
Name: MEDV, dtype: float64
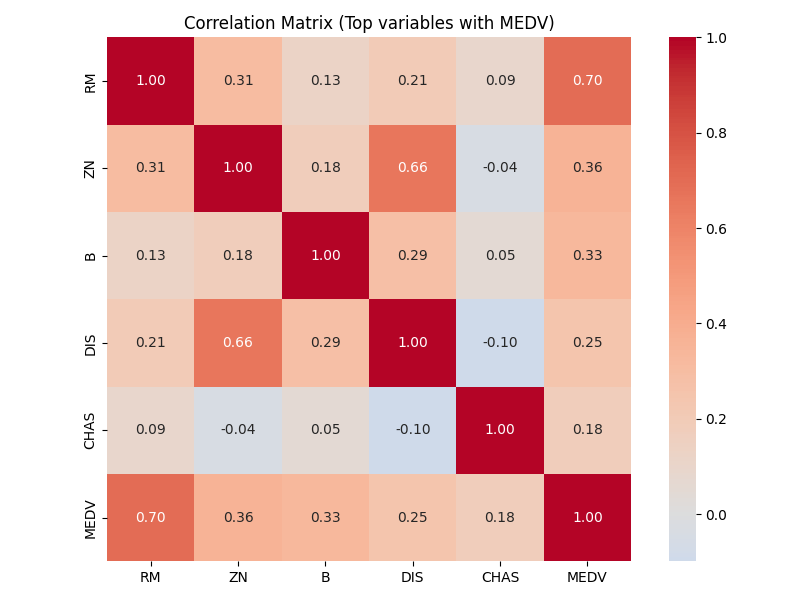
| 순위 | 변수 | 상관계수 | 변수 설명 |
|---|---|---|---|
| 1 | RM | 0.695 | 주택당 평균 방 개수 — 방이 많을수록 집값이 높아지는 경향 |
| 2 | ZN | 0.360 | 25,000 평방피트(약 2,323㎡) 이상의 대형 주택용 토지 비율 — 고급 주거지일수록 집값이 높음 |
| 3 | B | 0.333 | 흑인 인구 비율 기반 지표: 1000(Bk − 0.63)² — 인종 관련 지표로 당시 집값과 통계적 상관 |
| 4 | DIS | 0.250 | 보스턴 주요 고용 중심지까지의 거리 — 거리가 멀수록 선호도가 낮아질 수 있음 |
| 5 | CHAS | 0.175 | 찰스강 인접 여부 (1: 인접) — 강 인접 지역의 집값이 더 높음 |
분석 및 시사점(인사이트) 도출
Boston Housing 데이터셋의 상관분석 결과, 주택 가격(MEDV)과 가장 강한 양의 상관을 보이는 변수는 RM(주택당 평균 방 개수) 로, 상관계수는 약 0.70에 달한다. 이는 방의 개수가 많을수록 주택의 크기와 품질이 높아지며, 그에 따라 주택 가격 역시 상승하는 경향이 있다는 점을 시사한다. 실제로 고급 주택일수록 방의 수가 많고 넓은 평형을 갖추고 있기 때문에, RM은 주택 가격을 예측하는 데 있어 핵심적인 변수로 작용한다.
두 번째로 높은 상관을 보이는 ZN(대형 주택용 토지 비율) 변수는 특정 지역이 대규모 주택 부지로 지정되어 있을수록 해당 지역의 주택 가격이 높다는 점을 보여준다. 이는 도시 계획 및 토지 용도 구분이 부동산 가치 형성에 중요한 역할을 한다는 점을 반영하며, 고급 주택지일수록 ZN 값이 높게 나타난다.
세 번째로 높은 상관을 보이는 B(흑인 인구 비율 기반 지표) 는 당시의 사회적·인종적 요인과 주택 가격 간의 상관관계를 반영한다. B 값이 높다는 것은 Bk 값(흑인 인구 비율)이 특정 구간과의 차이가 작다는 것을 의미하며, 이는 역사적 맥락에서 주택 가격과 인종적 분포가 통계적으로 유의미한 상관성을 가졌음을 시사한다. 오늘날 이 변수는 지역 사회의 구조적 특성과 주거 환경의 사회적 맥락을 해석할 수 있는 지표로 활용될 수 있다.
네 번째 변수인 DIS(도심 주요 고용지로부터의 거리) 는 거리가 멀수록 주택 가격이 낮아지는 경향을 보여준다. 이는 도심 접근성이 높을수록 직장, 교통, 편의시설 등 다양한 요소에서 이점이 있어 부동산 가치가 높아진다는 도시 경제의 일반적 패턴을 잘 반영한다.
마지막으로 CHAS(찰스강 인접 여부) 는 강과 접한 주택지가 평균적으로 더 높은 가격을 형성한다는 점을 보여준다. 이는 수변 지역이 경관, 환경적 쾌적성, 프리미엄 이미지 등의 요인으로 인해 부동산 가치 상승에 긍정적인 영향을 미치는 전형적인 사례다.
요약하자면, 상위 5개 변수의 분석을 통해 주택 가격은 단순히 물리적 구조(RM)뿐만 아니라, 지역의 토지 이용 특성(ZN), 사회적·환경적 요인(B, DIS), 그리고 자연환경(CHAS) 등 복합적인 요소에 의해 결정된다는 것을 알 수 있다. 이는 회귀모델이나 예측 모델을 설계할 때, 단일 요인만이 아니라 공간적·사회적·환경적 변수들을 종합적으로 고려해야 함을 시사한다.
단순 회귀 분석
개념
단순 회귀분석(Simple Linear Regression) 은 하나의 독립 변수(Independent Variable) \(x\)와 종속 변수(Dependent Variable) \(y\) 사이의 선형 관계(Linear Relationship) 를 모델링하는 통계적 방법이다.
즉, \(x\)가 변할 때 \(y\)가 어떻게 변하는지를 하나의 직선(line) 으로 근사하여 예측하는 것이다.
예를 들어, 공부 시간(\(x\))과 시험 점수(\(y\)) 간의 관계를 생각해보자.
공부 시간이 많을수록 점수가 높아진다면, 두 변수 사이에는 양의 선형 관계가 존재한다.
이 관계를 수식으로 표현하면 다음과 같다.
수학적 표현식
- \(y\): 종속 변수 (예측하려는 값)
- \(x\): 독립 변수 (입력 또는 설명 변수)
- \(\beta_0\): 절편 (intercept) — \(x=0\)일 때의 \(y\) 값
- \(\beta_1\): 기울기 (slope) — \(x\)가 1 단위 증가할 때 \(y\)의 변화량
- \(\epsilon\): 오차항 (error term) — 실제 값과 예측 값의 차이, 데이터의 실제값 \(y\) 가 회귀선에서 얼마나 벗어나는지를 설명해주는 불확실성의 부분으로 \(\epsilon\) 값은 우리가 직접 알 수 없는 확률적 잡음(random noise)에 해당되므로 모델이 설명하지 못하는 부분을 의미함
회귀 분석의 목적은 주어진 데이터로부터 \(\beta_0\) 와 \(\beta_1\) 을 추정하여
데이터를 가장 잘 설명하는 회귀 직선(regression line) 을 찾는 것이다.
최소제곱법(OLS; Ordinary Least Squares)
회귀선은 모든 데이터 점들로부터의 거리(잔차, residual)가 최소가 되도록 설정된다.
즉, 각 점의 오차 제곱을 합한 값을 SSE (Sum of Squared Error) 최소화하는 방법을 최소제곱법(OLS) 이라고 한다.
MSE (Mean Squared Error)
잔차 제곱합을 데이터 개수 n으로 나눈 평균값, 즉 평균제곱오차이다. OLS의 평균을 구하는 점만 다를 뿐 최소화 되는 지점 (최적 회귀 계수 \(\beta_0\) 와 \(\beta_1\))는 동일하다.
시각적 이해
회귀선은 데이터의 전체적인 추세를 요약한다.
아래 그림은 데이터 포인트(파란색 점들)와 그에 가장 잘 맞는 회귀선(빨간색 선)을 보여준다.
import numpy as np
import matplotlib.pyplot as plt
# 샘플 데이터 생성
np.random.seed(42)
x = np.linspace(0, 10, 30)
y = 2.5 * x + np.random.randn(30) * 4 + 5 # y = 2.5x + 5 + noise
# 회귀선 계산
# np.polyfit(x, y, 1)
# → 주어진 데이터 (x, y)에 대해 1차 다항식(즉, 직선)을 가장 잘 맞추는
# 계수 [기울기(slope), 절편(intercept)]를 계산하는 함수
# → 내부적으로 최소제곱법(OLS)을 이용해 계수를 추정함
coef = np.polyfit(x, y, 1)
print(f"회귀 계수: {coef}")
# np.polyval(coef, x)
# → polyfit으로 구한 계수를 이용해 각 x값에 대응하는 y의 예측값(ŷ)을 계산
y_pred = np.polyval(coef, x)
plt.scatter(x, y, color='steelblue', label='데이터')
plt.plot(x, y_pred, color='red', linewidth=2, label='회귀선')
plt.xlabel('x (독립변수)')
plt.ylabel('y (종속변수)')
plt.title('단순 회귀 분석 예시')
plt.legend()
plt.show()
-
출력결과
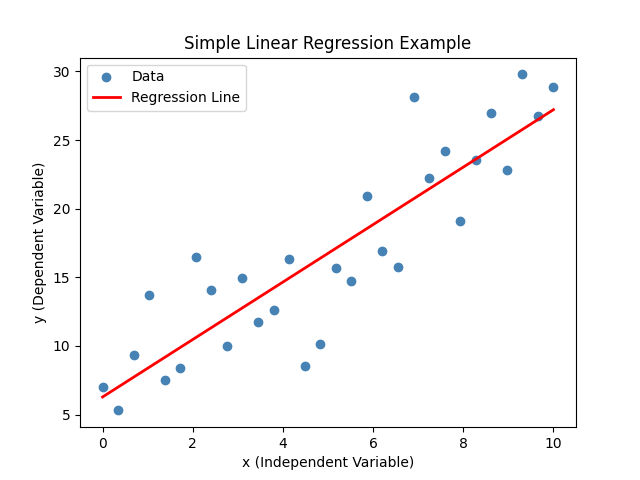
회귀 계수: [2.0923798 6.28551344]
\(y = 2.0923798x + 6.28551344\)를 의미한다.
Kaggle 데이터 분석: 자동차 연비 예측 (단순 회귀 분석)
문제 개요
자동차의 연비(MPG, Miles Per Gallon)는 엔진 성능과 차량의 물리적 특성에 따라 달라진다.
이번 실습에서는 Kaggle의 Auto MPG 데이터셋을 사용하여 엔진의 마력(horsepower) 이 연비(mpg, mile per gallon) 에 어떤 영향을 미치는지를 분석한다.
이를 통해 단순 회귀 분석(Simple Linear Regression)의 개념을 이해하고,
회귀 계수의 의미를 실제 데이터로 직관적으로 파악한다.
데이터셋 설명
| 변수명 | 설명 |
|---|---|
| mpg | 자동차의 연비 (Miles per gallon, 종속 변수) |
| cylinders | 실린더 수 |
| displacement | 배기량 (cubic inches) |
| horsepower | 마력 (horse power) |
| weight | 차량 무게 (lbs) |
| acceleration | 0→60mph 가속 시간 (seconds) |
| model year | 생산 연도 (model year) |
| origin | 생산 지역 코드 (1: 미국, 2: 유럽, 3: 일본) |
| car name | 차량 이름 |
데이터 다운로드: https://www.kaggle.com/datasets/uciml/autompg-dataset
-
직접 다운로드: click me
-
회원가입 및 로그인이 필요할 수 있음.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# Kaggle에서 다운로드한 CSV 파일 경로
DATA_PATH = "./auto-mpg.csv"
df = pd.read_csv(DATA_PATH)
print("데이터 크기:", df.shape)
print(df.head())
# 결측치 및 데이터 타입 확인
print("\n결측치 확인:")
print(df.isnull().sum())
# horsepower 컬럼은 Auto MPG 데이터셋에서 일부 값이
# 숫자가 아니라 문자열 '?' 로 되어 있기 때문에,
# 그대로는 숫자형 연산(상관계수, 회귀분석 등)을 할 수 없음
# 이를 해결하기 위해 pd.to_numeric()과 errors="coerce" 옵션을 사용
# | 옵션 | 설명 |
# | ---------- | -------------------------------------- |
# | `'ignore'` | 변환 불가능한 값은 그대로 둠 (문자열 유지) |
# | `'raise'` | 변환 불가능한 값이 있으면 오류 발생 |
# | `'coerce'` | 변환 불가능한 값을 **NaN (결측치)** 로 처리 |
df['horsepower'] = pd.to_numeric(df['horsepower'], errors='coerce')
# horsepower가 NaN인 행은 삭제
df = df.dropna(subset=['horsepower'])
print("\n변환 후 데이터 크기:", df.shape)
print(df[['mpg','horsepower']].describe())
- 실행 결과
데이터 크기: (398, 9)
mpg cylinders displacement horsepower weight acceleration model year origin car name
0 18.0 8 307.0 130 3504 12.0 70 1 chevrolet chevelle malibu
1 15.0 8 350.0 165 3693 11.5 70 1 buick skylark 320
2 18.0 8 318.0 150 3436 11.0 70 1 plymouth satellite
3 16.0 8 304.0 150 3433 12.0 70 1 amc rebel sst
4 17.0 8 302.0 140 3449 10.5 70 1 ford torino
결측치 확인:
mpg 0
cylinders 0
displacement 0
horsepower 0
weight 0
acceleration 0
model year 0
origin 0
car name 0
dtype: int64
변환 후 데이터 크기: (392, 9)
mpg horsepower
count 392.000000 392.000000
mean 23.445918 104.469388
std 7.805007 38.491160
min 9.000000 46.000000
25% 17.000000 75.000000
50% 22.750000 93.500000
75% 29.000000 126.000000
max 46.600000 230.000000
절편 (intercept): 39.93586102117047
기울기 (slope): -0.15784473335365365
R²: 0.606, RMSE: 4.893
# 이전 코드에 이어서 작성
X = df[['horsepower']].values
y = df['mpg'].values
model = LinearRegression()
model.fit(X, y)
print("절편 (intercept):", model.intercept_)
print("기울기 (slope):", model.coef_[0])
# 예측
y_pred = model.predict(X)
# 성능 지표
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
rmse = np.sqrt(mse)
print(f"R²: {r2:.3f}, RMSE: {rmse:.3f}")
- 출력결과
절편 (intercept): 39.93586102117047
기울기 (slope): -0.15784473335365365
R²: 0.606, RMSE: 4.893
R² (결정계수, Coefficient of Determination) 는 회귀 모델이 실제 데이터를 얼마나 잘 설명하는지를 나타내는 지표이다.
즉, 모델의 설명력(Goodness of Fit) 을 수치화한 값이다.
- SSE (Sum of Squared Errors): 예측값과 실제값 간의 오차 제곱합
- SST (Total Sum of Squares): 실제 데이터의 평균으로부터의 총 제곱합 (데이터의 전체 변동성)
해석 방법
| R² 값 | 해석 |
|---|---|
| 1.0 | 완벽한 예측 — 모든 데이터를 정확히 100% 설명함 |
| 0.7 | 데이터 변동의 70%를 모델이 설명하고,나머지 30%는 오차나 다른 요인에 의해 발생 |
| 0.0 | 모델이 평균보다 나은 설명력을 전혀 가지지 않음 |
| 음수 | 모델이 오히려 평균값보다 나쁜 예측을 함 (모델 부적합) |
자동차 연비 예측 모델에서 R² = 0.606 이라면, 다음과 같이 해석할 수 있다.
“차량의 마력(horsepower)만으로 연비(MPG) 변동의 약
60.6%를 설명할 수 있다.”
나머지40%는 차량 무게, 배기량, 운전 습관 등의 다른 요인에 의해 발생한다.
시각적 해석
-
데이터 점이 회귀선 주변에 밀집되어 있으면 → R²이 높음
-
데이터 점이 넓게 퍼져 있으면 → R²이 낮음
# 앞 코드에 이어서 작성
plt.figure(figsize=(8,6))
sns.scatterplot(
x='horsepower',
y='mpg',
data=df,
color='steelblue',
alpha=0.7,
label='Real Data'
)
sns.lineplot(
x=df['horsepower'],
y=y_pred,
color='red',
label='Regression line (Predicted ŷ)'
)
plt.title('Relation between Horsepower and MPG')
plt.xlabel('Horsepower')
plt.ylabel('MPG')
plt.legend()
plt.tight_layout()
plt.show()
-
출력결과
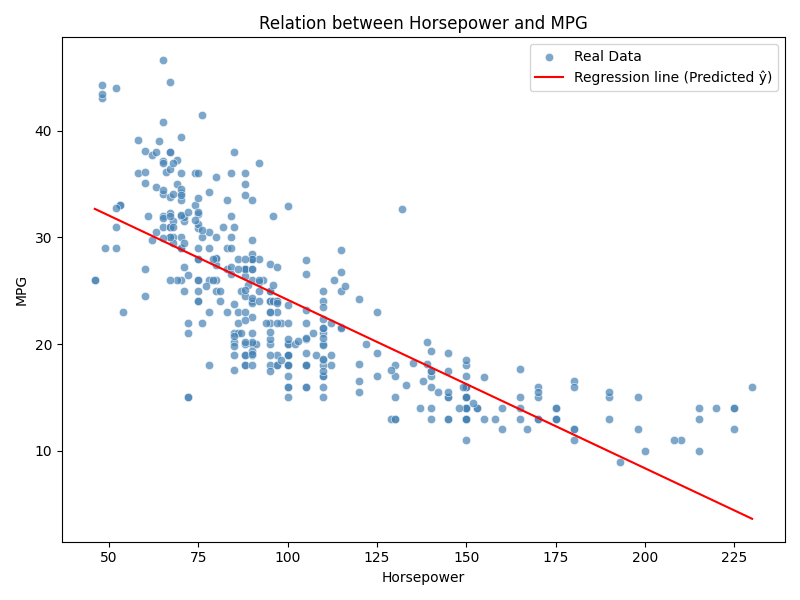
결과 해석
-
회귀식:
\( \hat{y} = 39.935 - 0.157x \) -
해석:
마력이 1 증가할 때마다 평균적으로 연비는 약 0.157 MPG 감소한다.
즉, 고성능(고마력) 차량일수록 연비 효율은 낮아지는 경향을 보인다. -
결정계수 R² = 0.606는, 연비의 약 60%가 마력 변수로 설명될 수 있음을 의미한다.
시사점 (Insights)
-
단순 회귀 분석을 통해 연비(MPG)가 마력에 음의 상관관계를 가지는 것을 확인했다.
-
마력 외에도 배기량, 무게 등 다른 변수들이 연비에 영향을 줄 수 있다.
-
다중 회귀 분석으로 확장하면 연비 예측 정확도를 높일 수 있다.
-
데이터 전처리(결측치 제거, 단위 변환)는 회귀 분석의 기본 전제 조건이다.
참고
-
단순 회귀는 두 변수의 선형 관계를 설명하는 가장 기본적인 회귀 기법이다.
-
예측식에는 오차항 \( \epsilon \) 이 포함되지 않는다.
\( \hat{y} = \beta_0 + \beta_1 x \)
-
최소제곱법(OLS)은 예측오차 제곱합(SSE)을 최소화하며, 이는 MSE 최소화와 동일한 원리다.
다중 회귀 분석
개념
단순 회귀분석이 하나의 독립 변수(x)가 종속 변수(y)에 미치는 영향을 분석한다면,
다중 회귀분석(Multiple Linear Regression) 은 두 개 이상의 독립 변수가
동시에 종속 변수에 어떤 영향을 미치는지를 분석한다.
즉, 여러 요인을 함께 고려해 종속 변수의 변동을 설명하고 예측 정확도를 높이는 모델이다.
수학적 표현식
- \(y\): 종속 변수 (예측 대상)
- \(x_1, x_2, ..., x_n\): 독립 변수들
- \(\beta_0\): 절편 (Intercept)
- \(\beta_i\): 각 독립 변수의 회귀계수 — 다른 변수들이 일정할 때, 해당 변수의 변화가 y에 미치는 영향
- \(\epsilon\): 오차항 — 모델이 설명하지 못하는 부분(잡음)
Kaggle 데이터 분석: 자동차 가격 예측 (다중 회귀)
문제 개요
자동차의 판매 가격은 엔진 크기, 마력, 연식, 브랜드 등 여러 요인의 영향을 받는다.
이번 실습에서는 Kaggle의 Car Price Prediction 데이터셋을 이용해
자동차 가격(price)이 어떤 변수들에 의해 설명되는지를 분석한다.
-
데이터셋 다운로드: https://www.kaggle.com/datasets/hellbuoy/car-price-prediction
- 직접 다운로드: click me
데이터셋 설명
| 변수명 | 설명 |
|---|---|
| symboling | 보험 위험 등급 |
| wheelbase | 축간 거리 (inch) |
| carlength, carwidth, carheight | 차량 크기 |
| curbweight | 공차중량 (lbs) |
| enginesize | 엔진 배기량 (cc) |
| horsepower | 마력 (hp) |
| peakrpm | 최대 회전수 (rpm) |
| citympg, highwaympg | 도심/고속도로 연비 |
| price | 자동차 판매가격 (종속변수) |
실습 단계
- 데이터 불러오기 및 확인
- 특징 변수 선택 (다중 독립변수 구성)
- 학습/검증 데이터 분리
- 모델 학습 및 회귀계수 해석
- 모델 성능 평가 (R², RMSE)
- 시각화 (실제 vs 예측 비교)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# 1. 데이터 로드
DATA_PATH = "./CarPrice_Assignment.csv"
df = pd.read_csv(DATA_PATH)
print("데이터 크기:", df.shape)
print(df[['price', 'enginesize', 'horsepower', 'curbweight', 'citympg']].head())
# 2. 주요 독립변수 선택
features = ['enginesize', 'horsepower', 'curbweight', 'citympg']
target = 'price'
X = df[features]
y = df[target]
# 3. 학습/검증 데이터 분리 (8:2 비율)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 4. 모델 학습
model = LinearRegression()
model.fit(X_train, y_train)
# 회귀계수 출력
coef_table = pd.DataFrame({
'Variable': features,
'Coefficient': model.coef_.round(3)
})
print("\n회귀계수:\n", coef_table)
print("절편 (Intercept):", round(model.intercept_, 3))
# 5. 예측 및 평가
y_pred = model.predict(X_test)
r2 = r2_score(y_test, y_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print(f"R²: {r2:.3f}, RMSE: {rmse:.2f}")
# 6. 실제값 vs 예측값 비교
plt.figure(figsize=(7,6))
sns.scatterplot(x=y_test, y=y_pred, color='steelblue', alpha=0.7)
plt.plot([y.min(), y.max()], [y.min(), y.max()], color='red', lw=2)
plt.xlabel("Actual Price")
plt.ylabel("Predicted Price")
plt.title("Actual vs Predicted Car Price")
plt.legend(['Actual Price', 'Predicted Price'])
plt.show()
실행 결과
데이터 크기: (205, 26)
price enginesize horsepower curbweight citympg
0 13495.0 130 111 2548 21
1 16500.0 130 111 2548 21
2 16500.0 152 154 2823 19
3 13950.0 109 102 2337 24
4 17450.0 136 115 2824 18
회귀계수:
Variable Coefficient
0 enginesize 80.397
1 horsepower 48.838
2 curbweight 3.936
3 citympg -47.919
절편 (Intercept): -10913.718
R²: 0.816, RMSE: 3814.81
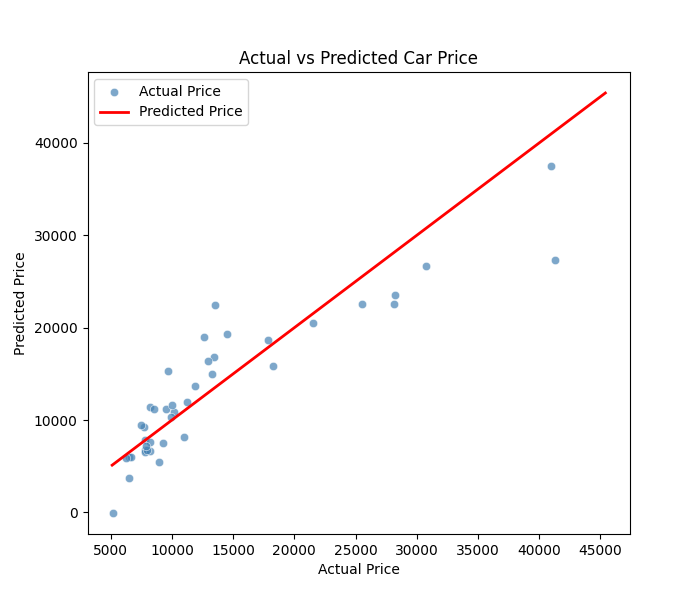
결과 해석
- 모델식
-
해석
-
엔진 크기(
enginesize)와 마력(horsepower)이 클수록 차량의 가격이 상승한다. -
차량 무게(
curbweight)가 높을수록 가격이 다소 상승하는 경향이 있다. -
연비(
citympg)가 높을수록(연비가 좋은 차일수록) 가격이 낮은 경향 — 고성능 차량일수록 연비가 낮기 때문이다.
-
-
R² = 0.816
-
모델이 자동차 가격 변동의 약 81.6%를 설명한다.
-
나머지 18.4%는 브랜드, 디자인, 옵션 등 비수치적 요인으로 설명 가능하다.
-
-
RMSE = 3814.81
- 예측 오차의 표준편차 수준이 약 3,800달러임을 의미한다.
시사점 (Insights)
-
단순회귀보다 높은 설명력을 보이며, 여러 요인을 동시에 고려하면 예측 정확도가 향상됨
-
각 변수의 회귀계수를 통해 가격에 미치는 상대적 영향력을 해석 가능
-
R²가 높더라도 잔차의 분포(Residual Plot) 점검을 통해 모델의 적합성을 추가로 평가해야 함
-
다중공선성(Multicollinearity)이 존재할 경우 변수 간 상관을 점검하고 제거해야 함
잔차 분석
잔차(Residual)의 개념
잔차(Residual) 는 실제값과 예측값의 차이를 의미한다.
$$
e_i = y_i - \hat{y}_i
$$
즉, 모델이 각 데이터 포인트를 얼마나 잘 예측했는지를 보여주는 지표이다.
회귀모델의 성능이 높더라도, 잔차의 분포를 분석해야 모델이 선형성을 가정한 것이 타당한지 확인할 수 있다.
이상적인 잔차의 특징
다중 선형회귀 모델이 적합하다면, 잔차는 다음과 같은 패턴을 보여야 한다:
| 조건 | 설명 |
|---|---|
| 평균이 0에 가까움 | 예측값과 실제값의 평균적인 차이가 거의 없음 |
| 등분산성 (Homoscedasticity) | 예측값의 크기에 따라 잔차의 분산이 일정해야 함 |
| 독립성 (Independence) | 잔차들이 서로 독립적이어야 함 (시간 순서나 패턴이 없어야 함) |
| 정규성 (Normality) | 잔차의 분포가 정규분포에 가까워야 함 |
잔차 시각화 실습 코드
# 다중 선형회귀 코드에 이어서 작성
import scipy.stats as stats
# 예측값과 잔차 계산
y_pred = model.predict(X_test)
residuals = y_test - y_pred
# 1. 잔차 vs 예측값
plt.figure(figsize=(7,5))
sns.scatterplot(x=y_pred, y=residuals, color="darkorange", alpha=0.7)
plt.axhline(y=0, color='navy', linestyle='--')
plt.xlabel("Predicted Price")
plt.ylabel("Residuals")
plt.title("Residuals vs Predicted Values")
plt.tight_layout()
plt.show()
# 2. 잔차의 분포 (정규성 확인)
plt.figure(figsize=(6,4))
sns.histplot(residuals, kde=True, bins=25, color="steelblue")
plt.title("Distribution of Residuals")
plt.xlabel("Residual")
plt.ylabel("Frequency")
plt.tight_layout()
plt.show()
# 3. Q-Q Plot (정규분포 적합성 검사)
plt.figure(figsize=(5,5))
stats.probplot(residuals, dist="norm", plot=plt)
plt.title("Q-Q Plot of Residuals")
plt.tight_layout()
plt.show()
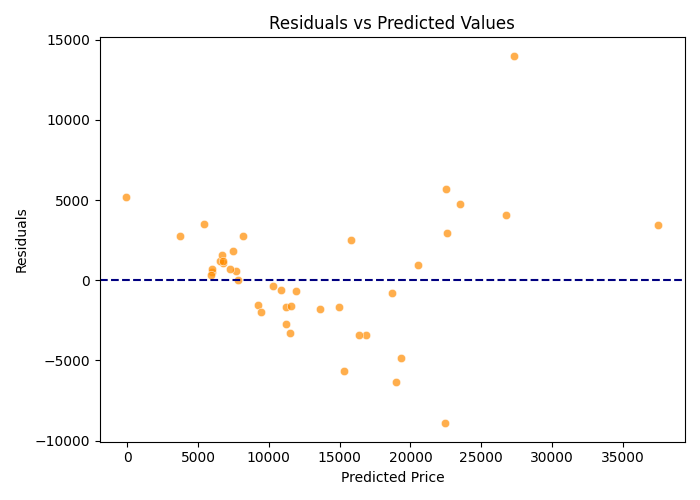
Residual vs. Predicted Plot
이 그래프는 모델의 예측값(가로축)에 대해 잔차(세로축)를 나타낸 것이다.
이때 잔차는 실제값과 예측값의 차이 (y - ŷ) 로,
모델이 각 데이터 포인트를 얼마나 정확히 예측했는지를 보여준다.
-
잔차의 평균이 0을 중심으로 분포
-
대부분의 점들이 파란 점선(잔차=0)을 중심으로 고르게 분포되어 있다.
-
모델이 전반적으로 과대 예측(overestimation) 또는 과소 예측(underestimation) 편향 없이 작동하고 있음을 의미한다.
-
-
잔차의 등분산성(Homoscedasticity)
-
예측값이 증가할수록 잔차의 분산이 다소 커지는 경향이 보인다.
-
일부 고가 차량에서 예측 오차가 커지는 이분산성(Heteroscedasticity) 징후가 관찰된다. 고가 차량일수록 모델이 가격 변동을 완전히 설명하지 못하고 있음을 시사한다.
-
-
비선형 패턴의 부재
-
잔차가 뚜렷한 곡선 형태를 보이지 않는다.
-
선형 관계(linearity) 가정은 대체로 타당하다고 판단할 수 있다.
-
-
이상치(Outliers) 존재 가능성
-
일부 점(예: 예측값이 30,000 이상이거나 잔차 ±10,000 근처)이 다른 분포로부터 떨어져 있다.
-
데이터 내 이상치(특이값)가 존재할 가능성을 보여주며, 이 값들이 회귀계수에 영향을 미쳤을 수 있다.
-
해석 요약
| 평가 항목 | 관찰 결과 | 해석 |
|---|---|---|
| 평균 중심성 | 잔차가 0을 중심으로 대체로 대칭적 | 편향 없는 모델 |
| 등분산성 | 고가 구간에서 분산 증가 | 이분산성 일부 존재 |
| 선형성 | 곡선 패턴 없음 | 선형 가정 타당 |
| 이상치 | 일부 극단값 존재 | 고가 차량 데이터 영향 가능성 |
Residual Distribution Plot
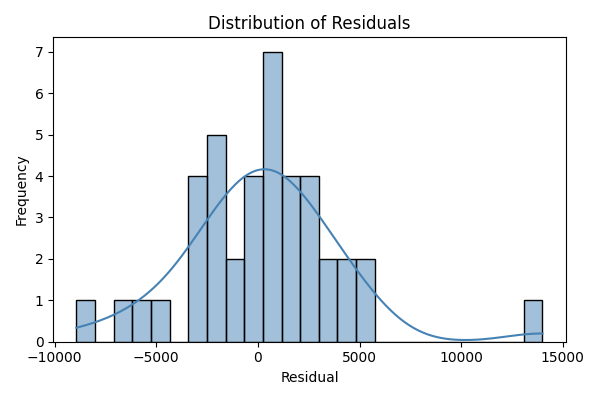
회귀모델에서 계산된 잔차(residuals) 들의 분포를 나타낸 것이다.
가로축은 잔차의 크기, 세로축은 해당 구간에 속한 데이터의 개수(빈도, Frequency)를 의미한다.
파란 곡선은 잔차의 커널 밀도(Kernel Density Estimation, KDE) 를 시각화한 것이다.
-
대체로 종 모양(Bell-shaped) 분포
-
잔차가 평균 0을 중심으로 좌우 대칭적인 형태를 보인다.
-
모델이 전체적으로 편향 없이 예측하고 있음을 의미한다.
-
-
정규성 가정(Normality) 대체로 만족
-
극단적인 잔차(±10,000 이상)는 일부 존재하지만, 대부분의 잔차가 0 부근에 집중되어 있다.
-
모델의 오차가 무작위적(random)으로 발생하고 있음을 보여준다.
-
-
약간의 오른쪽 꼬리(long right tail)
-
오른쪽으로 긴 꼬리가 형성되어 있어, 일부 예측값이 실제값보다 과소평가(underestimation) 되었음을 시사한다.
-
특히 고가 차량 데이터에서 예측 오차가 다소 크게 발생할 수 있다.
-
해석 요약
| 평가 항목 | 관찰 결과 | 해석 |
|---|---|---|
| 평균 중심성 | 잔차의 평균이 0 근처 | 예측에 편향 없음 |
| 분포 형태 | 약간의 비대칭, 종 모양 유지 | 정규성 대체로 만족 |
| 극단값 존재 | ±10,000 근처 일부 존재 | 고가 차량의 예측 오차 영향 가능성 |
**QQ plot of Residuals
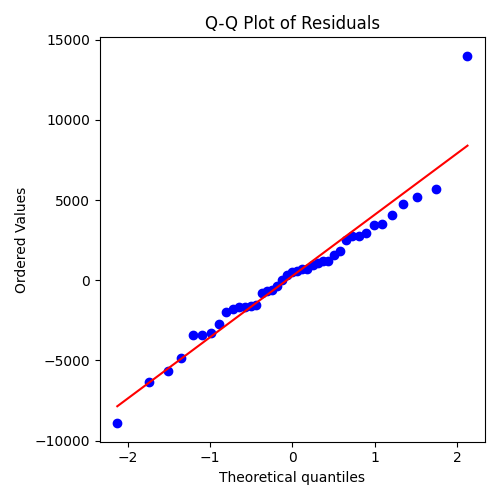
Q-Q(Quantile–Quantile) Plot은 회귀모델의 잔차(residuals)가 정규분포(normal distribution) 를 따르는지를 시각적으로 검증하기 위한 그래프이다.
가로축은 정규분포의 이론적 분위값(Theoretical Quantiles),
세로축은 실제 잔차의 분위값(Ordered Values)을 나타낸다.
빨간 선은 완벽한 정규분포를 따를 경우 점들이 위치해야 할 기준선이다.
-
중앙부의 점들이 대체로 직선에 근접
-
대부분의 점들이 빨간 기준선 위나 근처에 위치하고 있다.
-
잔차의 대부분이 정규분포를 잘 따르고 있음을 의미한다.
-
모델의 오차가 무작위적(Random) 이며 비편향적(Unbiased) 임을 시사한다.
-
-
양쪽 꼬리(Tails)에서 약간의 이탈
-
양 끝단 일부 점(특히 오른쪽 상단의 점)이 기준선에서 벗어나 있다.
-
극단적인 잔차(Outliers) 또는 고가 차량의 예측 오차 가능성이 존재한다.
-
실제 데이터 분포가 완전한 정규분포가 아니라 약간의 꼬리를 가짐을 보여준다.
-
-
전반적으로 정규성 가정(Normality assumption) 만족
-
중앙부에서 선형 패턴이 유지되므로,
-
선형 회귀 모델의 정규성 가정은 대체로 타당하다고 판단할 수 있다.
-
해석 요약
| 평가 항목 | 관찰 결과 | 해석 |
|---|---|---|
| 중앙부 패턴 | 직선에 근접 | 잔차 대부분이 정규분포 따름 |
| 꼬리 부분 | 약간 벗어남 | 일부 이상치 존재 |
| 전체 형태 | 전반적으로 직선형 | 정규성 가정 대체로 만족 |
시사점
-
단순히 R²가 높다고 해서 “좋은 모델”이라 단정할 수 없다.
-
잔차 분석을 통해 모델이 데이터의 패턴을 왜곡 없이 설명하는지 검증해야 한다.
-
잔차의 구조적 패턴이 보인다면,
-
변수 변환(log, sqrt 등)
-
이상치(Outlier) 처리
-
등의 방법으로 모델을 개선할 수 있다.