Numpy Practice & Excercise¶
Download source codes from github¶
Install Python virtual environment¶
- Linux or MacOS
python3 -m venv venv
Install Jupyter packages in your environment¶
activate your environment
- Linux or MacOS
source venv/bin/activate
- Windows
venv\Scripts\activate
- Linux or MacOS
Install Jupyter packages
(venv) pip install jupyter
Jupyter Editor Setting¶
We will use VSCode as the default editor for Jupyter Notebook.
To do this, we need to install the
jupyterextension.Browse Jupyter Notebook Extension
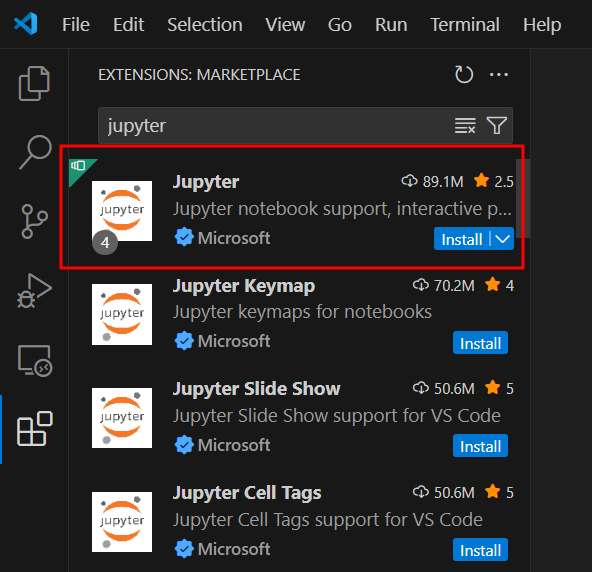
- Install Jupyter Notebook Extension
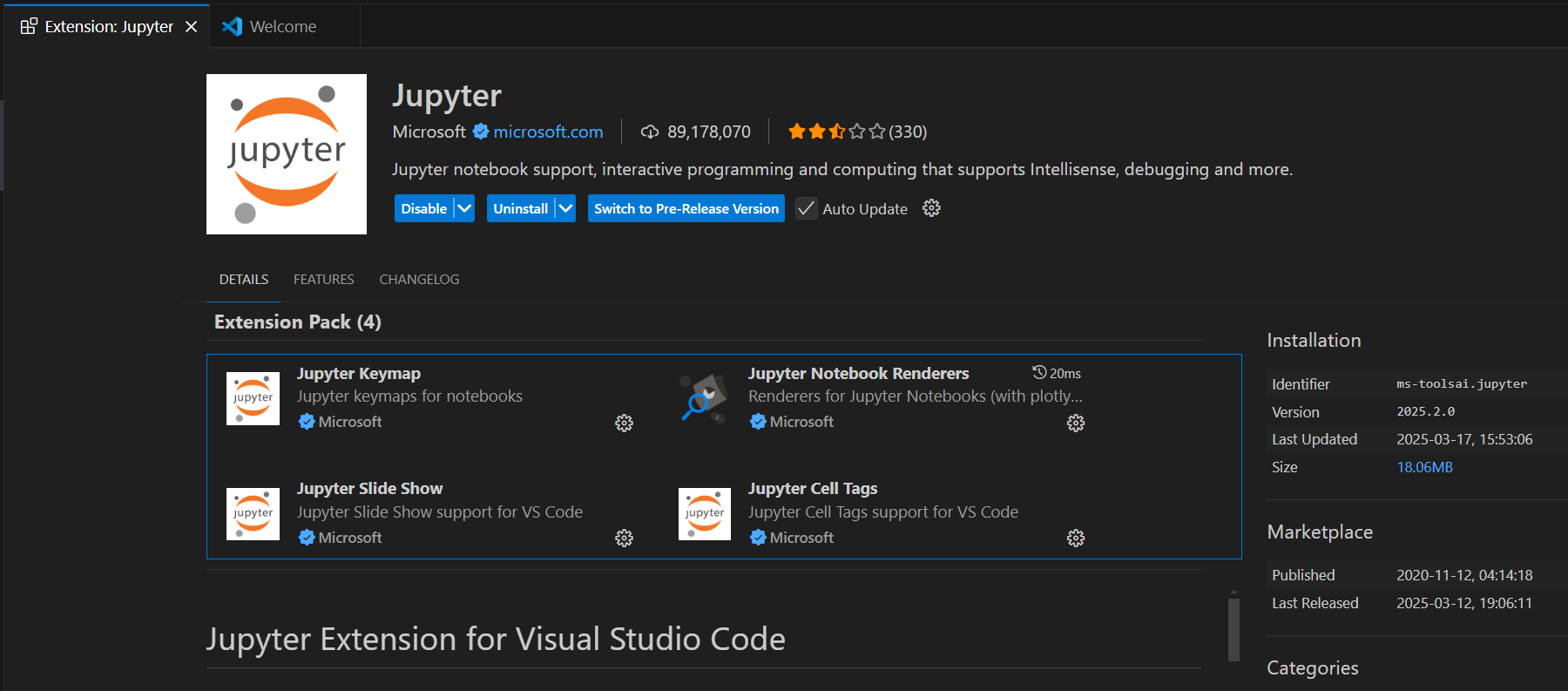
Install ipykernel in the VS Code Jupyter Notebook¶
- It may takes a few minutes to install the ipykernel in the VS Code Jupyter Notebook
1. Import the NumPy¶
The NumPy library is widely used in machine learning-related code as it enables various mathematical operations on arrays.
The following site is the official NumPy documentation.
If you want to learn more about NumPy, you can visit this site for further information.
- If required, install numpy in your environment
pip install numpy
In [ ]:
# Import the NumPy library and redefine it as np.
import numpy as np
In [ ]:
# Define print_obj() function to print objects.
def print_obj(obj, name):
print(name)
print(f'{obj}\n')
2. Scalars, Vectors, Matrices¶
In [ ]:
# Define arrays in the form of scalar, vector, and matrix.
array0 = np.array(1.) # 0 dimension array, scalar
array1 = np.array([1., 2., 3.]) # 1 dimension array, vector
array2 = np.array([[1., 2., 3.], [4., 5., 6.]]) # 2 dimension array, matrix
# print the arrays using the print_obj() function.
print_obj(array0, "scalar")
print_obj(array1, "vector")
print_obj(array2, "matrix")
In [ ]:
# print the dimension of each array.
# ndim → return the number of dimensions of an array.
print_obj(array0.ndim, "dimension of scalar")
print_obj(array1.ndim, "dimension of vector")
print_obj(array2.ndim, "dimension of matrix")
In [ ]:
# print the shape of each array.
print_obj(array0.shape, "shape of array0")
print_obj(array1.shape, "shape of array1")
print_obj(array2.shape, "shape of array2")
array3 = np.array([[1, 2, 3]])
print_obj(array3.shape, "shape of array3")
3. Tensors¶
In [ ]:
# Define tensors in the form of 3D and 4D arrays.
# 3D tensor
# 3D tensor is a 2D tensor with multiple samples.
tensor1 = np.array([[[1., 2., 3.], [4., 5., 6.]], [[7., 8., 9.], [10., 11., 12.]]])
# 4D tensor
# 4D tensor is a 3D tensor with multiple samples.
tensor2 = np.array([[[[1., 2., 3.], [1., 2., 3.]], [[4., 5., 6.], [4., 5., 6.]]],
[[[7., 8., 9.], [7., 8., 9.]], [[10., 11., 12.], [10., 11., 12.]]]])
# print the tensors using the print_obj() function.
print_obj(tensor1, "tensor1")
print_obj(tensor1.ndim, "tensor1.ndim")
print_obj(tensor1.shape, "tensor1.shape")
print_obj(tensor2, "tensor2")
print_obj(tensor2.ndim, "tensor2.ndim")
print_obj(tensor2.shape, "tensor2.shape")
4. Numpy arrays¶
- Numpy supports
- high performance array operations
- Neumerous built-in functions (very useful)
- Difference between list & array
- python list: don't need to be same data type
- numpy arrray: Contianing all same data type
In [ ]:
# Create a vector of 10 elements with all elements being 1.
# 원소가 1이고 크기가 10인 벡터를 넘파이 배열로 생성한다.
ones = np.ones(10)
print_obj(ones, "np.ones(10)")
In [ ]:
#
# 원소가 0이고 크기가 2x5인 행렬을 넘파이 배열로 생성한다.
# Create a 2x5 matrix with all elements being 0.
zeros = np.zeros((2, 5))
print_obj(zeros, "np.zeros((2, 5))")
In [ ]:
# 파라미터에 배열의 크기와 값을 입력한다.
# Create a 2x5 matrix with all elements being 5.
# 입력된 크기만큼의 배열을 만들고 입력한 값으로 배열을 채운다.
full = np.full((2, 5), 5)
print_obj(full, "np.full((2, 5), 5)")
# Create a 1x1x1 matrix with all elements being -1.
full2 = np.full((1, 1, 1), -1)
print_obj(full2, "np.full((1, 1, 1), -1)")
In [ ]:
# Create a 2x3x4 matrix with random values.
random = np.random.random((2, 3, 4))
print_obj(random, "np.random.random((2, 3, 4))")
In [ ]:
# Create a array with values from 0 to 9.
arange = np.arange(10)
print_obj(arange, "np.arange(10)")
In [ ]:
# Change the data type of the array to float.
# 배열의 데이터 타입을 변경
astype = np.arange(10).astype(float)
print_obj(astype, "np.arange(10).astype(float)")
In [ ]:
# Reshape a 1x10 array to a 2x5 array.
# 배열의 크기를 변경한다.
reshape = np.arange(10).reshape((5,2))
print_obj(reshape, "np.arange(10).reshape((5,2)")
5. Indexing & Slicing¶
In [ ]:
# Index is a number that indicates the position of an element in an array.
# One can access the data in an array using an index.
# Typically, an index greater than or equal to 0 means accessing from the front, and an index less than 0 means accessing from the back.
array_index = np.arange(10)
print_obj(array_index, "np.arange(10)")
print_obj(array_index[0], "array_index[0]")
print_obj(array_index[1], "array_index[1]")
print_obj(array_index[-1], "array_index[-1]")
print_obj(array_index[-3], "array_index[-3]")
In [ ]:
# range type index can be specified using a colon(:).
# The colon(:) is used to specify the range of indices.
print_obj(array_index[0:10], "array_index[0:10]")
print_obj(array_index[0:], "array_index[0:]")
print_obj(array_index[:],"array_index[:]")
print_obj(array_index[:10], "array_index[:10]")
print_obj(array_index[7:], "array_index[7:]")
print_obj(array_index[:5], "array_index[:5]")
print_obj(array_index[2:5], "array_index[2:5]")
In [ ]:
# The number after the last colon indicates the step if two colons are used in a single index.
# 하나의 인덱스에 두 개의 콜론(:)이 사용된다면, 마지막 콜론 뒤의 숫자는 스텝을 의미한다.
# The step indicates how much to skip when accessing data within the indexing range.
# 스텝은 인덱싱 범위 내에서 얼마만큼 건너뛰며 데이터에 접근할 것인지를 의미한다.
print_obj(array_index[0:10:2], "array_index[0:10:2]")
print_obj(array_index[0:10:3], "array_index[0:10:3]")
print_obj(array_index[2:6:3], "array_index[2:6:3]")
print_obj(array_index[::-1], "array_index[::-1]")
print_obj(array_index[8:5:-1], "array_index[8:5:-1]")
print_obj(array_index[8:5], "array_index[8:5]")
In [ ]:
# Indexing can be applied to multi-dimensional arrays.
array_index = np.arange(9).reshape((3,3))
print_obj(array_index, "array_index")
print_obj(array_index[0][0], "array_index[0][0]")
print_obj(array_index[0,0], "array_index[0,0]")
print_obj(array_index[1,1], "array_index[1,1]")
In [ ]:
# Slicing can be applied to multi-dimensional arrays.
array_index = np.arange(24).reshape((6, 4))
print_obj(array_index, "array_index")
print_obj(array_index[:,[0, 3]], "array_index[idx]")
print_obj(array_index[[0, 2, 3], :], "array_index[idx]")
In [ ]:
# Indexing can be applied to multi-dimensional arrays.
array_index = np.arange(4*3*2).reshape((4, 3, 2))
print_obj(array_index, "array_index")
print_obj(array_index[2, 1, 0], "array_index[2, 1, 0]")
6. Math Operations¶
In [ ]:
mat1 = np.arange(6).reshape((3, 2))
mat2 = np.ones((3, 2))
print_obj(mat1, "mat1")
print_obj(mat2, "mat2")
# +, -, *, / are elementwise operations.
# +, -, *, / 는 요소별 연산
print_obj(mat1 + mat2, "mat1 + mat2")
print_obj(mat1 - mat2, "mat1 - mat2")
print_obj(mat1 * mat2, "mat1 * mat2")
print_obj(mat1 / mat2, "mat1 / mat2")
In [ ]:
mat = np.arange(6).reshape((3, 2))
print_obj(mat, "mat")
print_obj(mat.sum(), "mat.sum()")
print_obj(mat.sum(axis=0), "mat.sum(axis=0)") # axis는 축을 의미
print_obj(mat.sum(axis=1), "mat.sum(axis=1)")
print_obj(mat.mean(), "mat.mean()")
print_obj(mat.max(), "mat.max()")
print_obj(mat.min(), "mat.min()")
In [ ]:
# Dot product of two arrays.
# 두 배열의 내적
mat1 = np.arange(3).astype('float')
mat2 = np.ones(3)
print_obj(mat1, "mat1")
print_obj(mat2, "mat2")
print_obj(np.dot(mat1, mat2), "mat1 dot mat2")
In [ ]:
mat1 = np.arange(6).reshape((3, 2))
mat2 = np.ones((2, 3))
print_obj(mat1, "mat1")
print_obj(mat2, "mat2")
print_obj(np.dot(mat1, mat2), "mat1 dot mat2")
print_obj(mat1 @ mat2, "mat1 @ mat2")
print_obj(np.matmul(mat1, mat2), "matmul(mat1, mat2)")
mat3 = np.arange(24).reshape((4, 3, 2))
mat4 = np.ones((4, 2, 3))
print_obj(mat3, "mat3")
print_obj(mat4, "mat4")
print_obj(np.dot(mat3, mat4).shape, "mat3 dot mat4") # dot 함수는 내적을 의미
print_obj((mat3 @ mat4).shape, "mat3 @ mat4") # @ 연산자는 행렬곱을 의미
print_obj(np.matmul(mat3, mat4).shape, "matmul(mat3, mat4)") # matmul 함수는 행렬곱을 의미
7. Shape Manipulation¶
In [ ]:
array1 = np.arange(24).reshape((2, 3, 4))
print_obj(array1, "np.arange(24).reshape((2, 3, 4))")
array2 = array1.reshape((6, 4))
print_obj(array2, "array1.reshape((6, 4))")
# -1 means the dimension is inferred from the remaining dimensions.
# -1은 나머지 차원에서 유추 -> 원하는 차원을 먼저 채우고, -1에 해당하는 차원을 나머지 차원에서 유추한다.
array3 = array1.reshape((6, -1))
print_obj(array3, "array1.reshape((6, -1))")
array4 = array1.reshape((-1, 6))
print_obj(array4, "array1.reshape((-1, 6))")
In [ ]:
array = np.arange(3)
print_obj(array, "array")
# By using None, the array is converted into a 2D array.
# None을 사용하여 배열을 2D 배열로 변환한다.
print_obj(array[:, None], "array[:, None]")
In [ ]:
array1 = np.ones((3, 2))
array2 = np.zeros((3, 2))
print_obj(array1, "array1")
print_obj(array2, "array2")
# Stack arrays in sequence vertically (row wise).
# 배열을 수직으로 쌓는다.
print_obj(np.vstack([array1, array2]), "array1 + 2 -> vstack")
# Stack arrays in sequence horizontally (column wise).
# 배열을 수평으로 쌓는다.
print_obj(np.hstack([array1, array2]), "array1 + 2 -> hstack")
print_obj(np.hstack([array1, array2, array1]), "array1 + 2 + 1 -> hstack")
# axis = 0 means stacking vertically and axis = 1 means stacking horizontally.
# axis = 0은 수직으로 쌓는 것을 의미하고, axis = 1은 수평으로 쌓는 것을 의미한다.
print_obj(np.concatenate([array1, array2], axis=0), "array1 + 2 concat axis = 0")
print_obj(np.concatenate([array1, array2], axis=1), "array1 + 2 concat axis = 1")
In [ ]:
# Transpose of an array.
# 배열의 전치
array = np.arange(6).reshape((3, 2))
print_obj(array, "array")
print_obj(array.T, "array.T")
In [ ]:
# Transpose of a multi-dimensional array.
# 다차원 배열의 전치
array1 = np.arange(24).reshape((4, 3, 2))
print_obj(array1, "array1")
array2 = np.transpose(array1, [0, 2, 1])
print_obj(array2, "Swap axis 1 and 2")
print_obj(array2.shape, "Swapped shape")
array3 = np.transpose(array1, [1, 0, 2])
print_obj(array3, "Swap axis 0 and 1")
print_obj(array3.shape, "Swapped shape")
8. Broadcasting¶
In [ ]:
vector = np.arange(3)
scalar = 2.
print_obj(vector, "vector")
print_obj(scalar, "scalar")
print_obj(vector + scalar, "vector + scalar")
print_obj(vector - scalar, "vector - scalar")
print_obj(vector * scalar, "vector * scalar")
print_obj(vector / scalar, "vector / scalar")
In [ ]:
mat1 = np.arange(6).reshape((3, 2))
mat2 = np.arange(2).reshape(2) + 1
print_obj(mat1, "mat1")
print_obj(mat2, "mat2")
print_obj(mat1 + mat2, "mat1 + mat2")
mat3 = np.arange(12).reshape((2, 3, 2))
mat4 = np.arange(6).reshape((3, 2))
print_obj(mat3, "mat3")
print_obj(mat4, "mat4")
print_obj(mat3 + mat4, "mat3 + mat4")